الگوریتم یادگیری وزن دار محلی (LWL)
سرفصل مطالب
الگوریتم یادگیری وزن دار محلی (LWL)
الگوریتم یادگیری وزن دار محلی (LWL) Locally Weighted Learning : یکی از الگوریتم های مهم در دنیای یادگیری ماشین الگوریتم رگرسیون است. این الگوریتم به دلیل کاربرد مختلف، بسیار استفاده می شود. به کار بردن این الگوریتم در دیتاست های مختلف باعث این شده که افزونه هایی زیادی برای این الگوریتم ایجاد شود. یکی از کاربردی ترین افزونه های این الگوریتم، الگوریتم رگرسیون مبتنی بر وزن محلی است که در این مطلب به بررسی آن می پردازیم.
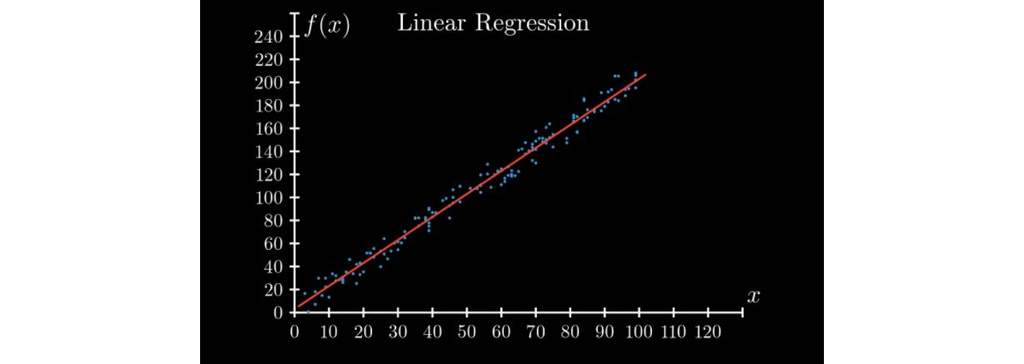
الگوریتم رگرسیون
فرض کنید یک مجموعه داده شامل برخی مقادیر متغیر مستقل (x)و مقداری خروجی وابسته به متغیر مستقل در قالب f (x) به ما ارائه شده است. گزاره مسئله این است که مقدار تقریبی f (x) را در برخی از x های داده شده محاسبه کنید. این مشکل در یادگیری ماشین، رگرسیون نامیده می شود. وقتی f (x) ماهیتی خطی داشته باشد، تبدیل به یک رگرسیون خطی می شود.
الگوریتم یادگیری وزن دار محلی (LWL)
الگوریتم یادگیری وزن دار محلی (LWL) : ما به دنبال چند نقطه داده از مجموعه نقاط داده شده هستیم که در مجاورت نقطه آزمایش قرار دارند و برای پیش بینی خروجی، آن نقاط را به نحوی (ساده وزن دار می کنیم).
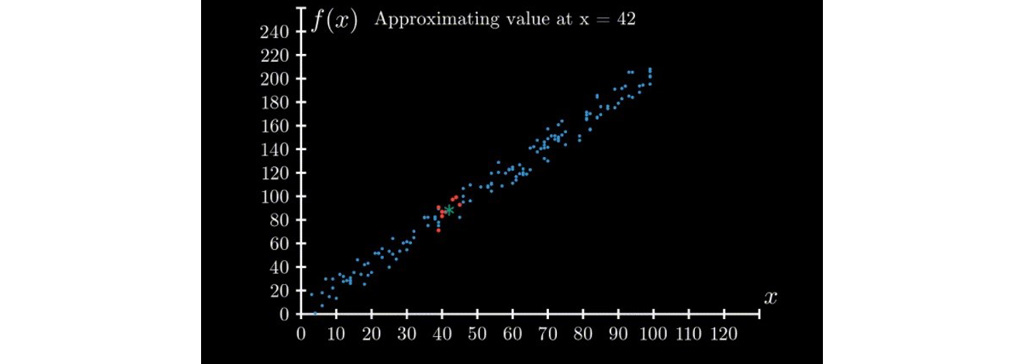
مثال الگوریتم یادگیری وزن دار محلی (LWL)
در زیر مثال الگوریتم یادگیری وزن دار محلی (LWL) است که ایده اصلی الگوریتم ها را نشان می دهد فرض کنید می خواهیم مقدار f (x) را در x = 42 محاسبه کنیم. برای محاسبه این مقدار دو مرحله زیر را دنبال می کنیم: 8 نقطه را انتخاب کنید که در مجموعه داده ما نزدیک 42 هستند. میانگین مقادیر f (x) نقاط انتخاب شده در اولین مراحل را محاسبه کنید.
این ایده اصلی الگوریتم یادگیری وزن دار محلی (LWL) است. نسخه های اصلاح شده زیادی از این ایده قدرتمند وجود دارد. این الگوریتم در مورد مجموعه داده های سری زمانی مانند مجموعه داده های حداقل دمای روزانه بسیار عالی عمل می کند.
رگرسیون مبتنی بر وزن محلی
جایگزین رگرسیون خطی برای تحلیل داده هایی با توزیع های مختلف
فرض اساسی برای رگرسیون خطی این است که داده ها باید بصورت خطی توزیع شوند. اما اگر داده ها بصورت خطی توزیع نشوند چه اتفاقی می افتد. آیا هنوز می توان ایده رگرسیون را به کار بست؟ و پاسخ بله است … ما می توانیم از رگرسیون استفاده کنیم و به آن رگرسیون مبتنی بر وزن محلی می گویند. هنگامی که رابطه بین متغیرهای مستقل و وابسته غیر خطی است، می توانیم ( LOWESS یا LOESS) یا همسان سازی پراکندگی با وزن محلی را اعمال کنیم.
تاریخچه الگوریتم یادگیری وزن دار محلی (LWL)
در سال 1964، ساویتسکی و گولای روشی معادل LOESS را پیشنهاد کردند که معمولاً از آن به عنوان فیلتر ساویتزکی -گلای یاد می شود. ویلیام اس کلیولند این روش را در سال 1979 دوباره کشف کرد و نام متمایزی بر آن گذاشت. این روش توسط کلیولند و سوزان ج.دولین (1988) بیشتر توسعه یافت. LOWESS به عنوان رگرسیون چند جمله ای با وزن محلی نیز شناخته می شود.
LOESS یا LOWESS
LOESS یا LOWESS روش های رگرسیون غیر پارامتری هستند که مدل های رگرسیون چندگانه را با یک متا مدل مبتنی برk نزدیکترین همسایگی ترکیب می کنند. آن ها به موقعیت هایی می پردازند که در آن ها روش های کلاسیک به خوبی عمل نمی کنند یا نمی توانند بدون کار غیر ضروری به طور موثر اعمال شوند. LOESS سادگی رگرسیون بر پایه حداقل مربعات خطا را با انعطاف پذیری رگرسیون غیر خطی ترکیب می کند. این کار را با تطبیق مدل های ساده با زیر مجموعه های محلی داده ها انجام می دهد تا عملکردی را ایجاد کند که تنوع داده ها را نقطه به نقطه توصیف می کند. در واقع، یکی از جذابیت های اصلی این روش این است که تحلیلگر داده ها ملزم به مشخص کردن یک عملکرد عمومی از هر شکلی نیست تا یک مدل را با داده ها مطابقت دهد، فقط برای تناسب بخش هایی از داده ها باید این کار را انجام دهد.
مبادله این ویژگی ها منجر به افزایش محاسبات است. از آنجایی که رگرسیون مبتنی بر وزن محلی از نظر محاسباتی بسیار فشرده است، استفاده از LOESS در عصری که رگرسیون حداقل مربعات در حال توسعه بود عملاً غیرممکن بود. اکثر روش های مدرن دیگر برای مدل سازی فرآیند از این نظر شبیه LOESS هستند. این روش ها به طور آگاهانه طراحی شده اند تا از توانایی محاسباتی فعلی ما به حداکثر استفاده کنند تا به اهدافی دست یابند که به راحتی با رویکردهای سنتی به دست نمی آیند.
در هر نقطه از محدوده مجموعه داده ها، چند جمله ای درجه پایین بر روی زیرمجموعه ای از داده ها اعمال می شود که دارای مقادیر متغیر توضیحی در نزدیکی نقطه ای است که پاسخ آن محاسبه می شود. چند جمله ای با استفاده از حداقل مربعات وزنی برازش شده است و وزن بیشتری را به نقاط نزدیک به نقطه ای که پاسخ آن برآورد می شود و وزن کمتری به نقاط دورتر می دهد. سپس مقدار تابع رگرسیون برای نقطه با ارزیابی چند جمله ای محلی با استفاده از مقادیر متغیر توضیحی برای آن نقطه داده به دست می آید. تناسب LOESS پس از محاسبه مقادیر تابع رگرسیون برای هر یک از n نقاط داده کامل می شود. بسیاری از جزئیات این روش مانند درجه مدل چند جمله ای و وزن ها قابل انعطاف است.
 مقایسه روش های عمومی و رگرسیون با وزن محلی
مقایسه روش های عمومی و رگرسیون با وزن محلی
عیب روش های عمومی این است که گاهی اوقات هیچ مقدار پارامتری نمی تواند تقریب کافی را ارائه دهد. جایگزینی برای تقریب عملکرد عمومی، یادگیری با وزن محلی یا LOWESS است. روش های یادگیری وزنی محلی غیر پارامتری هستند و پیش بینی فعلی توسط توابع محلی انجام می شود. ایده اصلی پشت LWL این است که به جای ایجاد یک مدل عمومی برای کل فضای عملکرد، برای هر نقطه مورد علاقه یک مدل محلی بر اساس داده های همسایه از داده آزمون ایجاد می شود. برای این منظور، هر نقطه داده به یک عامل وزنی تبدیل می شود که تأثیر نقطه داده را برای پیش بینی بیان می کند.
به طور کلی، نقاط داده ای که در مجاورت داده آزمون کنونی قرار دارند، وزن بیشتری نسبت به نقاط داده ای که دور هستند دریافت می کنند. LWL همچنین یادگیری کند نامیده می شود زیرا سرعت پردازش داده های آموزش تغییر می کند تا جایی که نیاز به پاسخ و پرسش باشد. این رویکرد LWL را به یک روش تقریب عملکرد بسیار دقیق تبدیل می کند که در آن افزودن داده های آموزشی جدید آسان است.
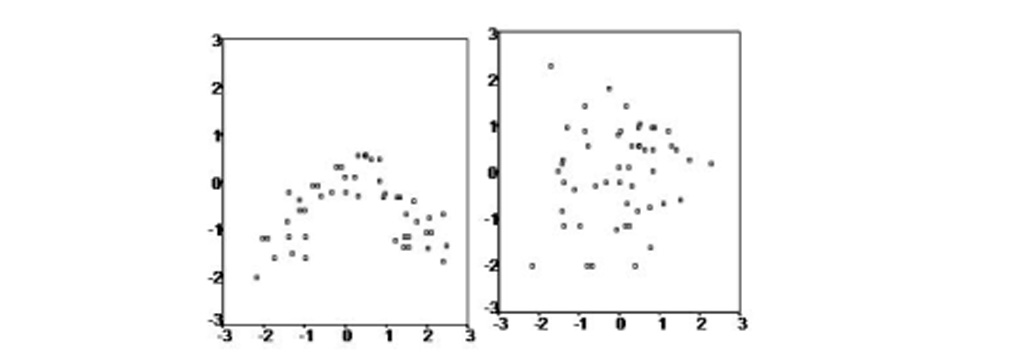
مثال الگوریتم رگرسیون با وزن محلی
در شکل زیر مجموعه داده ای را می بینیم که به صورت پراکنده است و به سختی می توان رابطه ای بین داده ها تعیین کرد که بتواند به پیش بینی مقادیر جدید به ما کمک کند. در ادامه مطلب به بررسی این دیتاست و الگوریتم رگرسیون با وزن محلی می پردازیم.
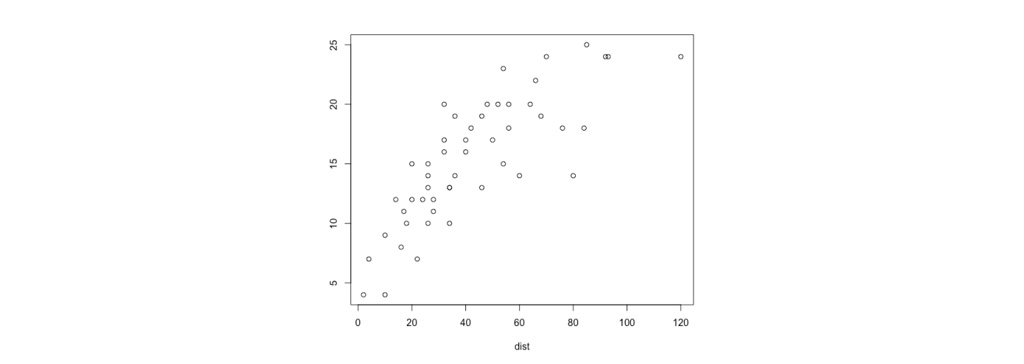
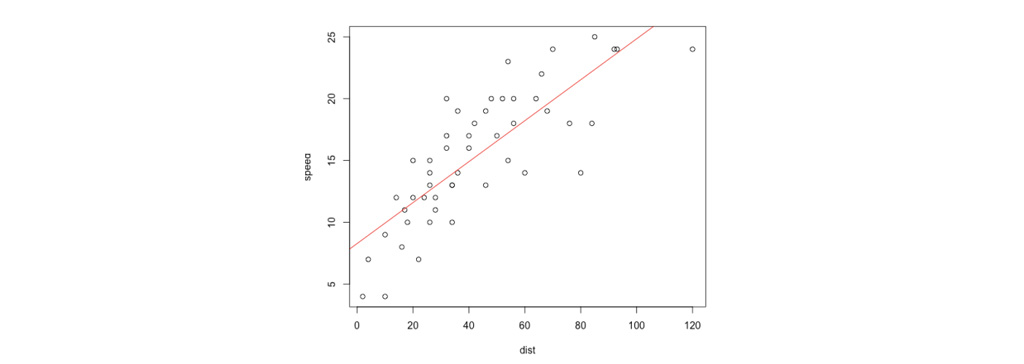
در الگوریتم رگرسیون خطی اصلی، برای پیش بینی در نقطه پرس و جو(x) به عنوان مثال ارزیابی h(x) باید به صورت زیر عمل کنیم:
- متناسب را به گونه ای پیدا کنیم تا معادله حداقل مربعات خطا را مینیم کند.
- مقدار خروجی الگوریتم باید مقدار هدف را پیش بینی کند.
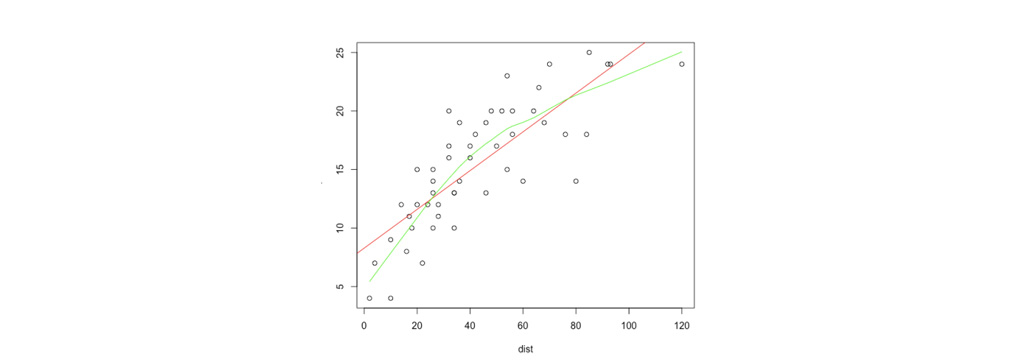
در مقابل ، الگوریتم رگرسیون خطی با وزن محلی موارد زیر را انجام می دهد:
- θ مناسب برای به حداقل رساندن خطایw (i) در مجموع مربع (جایی که w (i) برای وزن ها مقدار منفی است) محاسبه کند.
- مقدار خروجی الگوریتم باید مقدار هدف را پیش بینی کند.
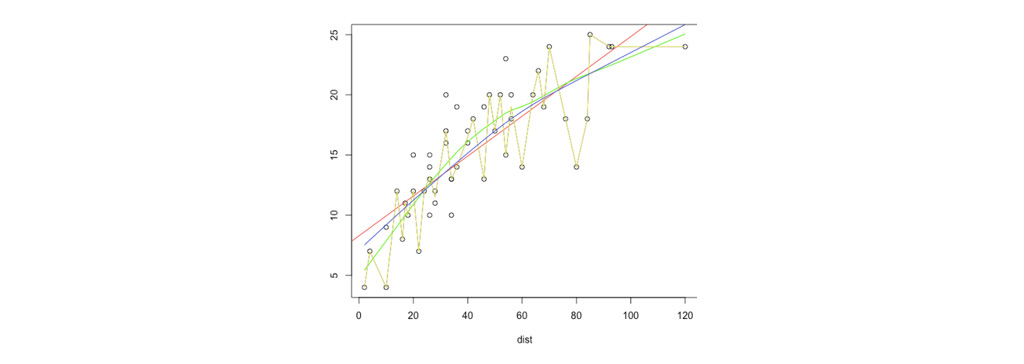
مقدار وزن استاندارد از معادله زیر محاسبه می شود.
 مزیت الگوریتم رگرسیون محلی مبتنی بر وزن
مزیت الگوریتم رگرسیون محلی مبتنی بر وزن
مزیت الگوریتم رگرسیون محلی مبتنی بر وزن : همانطور که در بالا مورد بحث قرار گرفت، بزرگترین مزیت LOESS نسبت به بسیاری از روش های دیگر این است که فرایند تطبیق یک مدل با داده های نمونه با مشخص کردن یک تابع آغاز نمی شود. در عوض، تحلیلگر فقط باید مقدار پارامتر هموار کننده و درجه چند جمله ای محلی را ارائه دهد. علاوه بر این، LOESS بسیار انعطاف پذیر است و برای مدل سازی فرآیندهای پیچیده ای که هیچ مدل نظری برای آنها وجود ندارد، ایده آل است. این دو مزیت، همراه با سادگی روش، LOESS را به یکی از جذاب ترین روش های رگرسیون مدرن برای برنامه هایی تبدیل می کند که با چارچوب کلی رگرسیون حداقل مربعات مطابقت دارند اما دارای ساختار قطعی پیچیده هستند.
اگرچه این روش نسبت به سایر روش های مربوط به رگرسیون حداقل مربعات خطا کمتر شناخته شده است، اما LOESS همچنین بیشترین میزان صحت در پیش بینی را که معمولاً توسط این روش ها به دست می آید را محاسبه می کند. مهم ترین آن ها نظریه محاسبه عدم قطعیت برای پیش بینی و کالیبراسیون است. بسیاری از آزمون ها و روش های دیگر که برای اعتبار سنجی مدل های حداقل مربع استفاده می شوند، می توانند به مدل های LOESS نیز تعمیم داده شوند.
معایب الگوریتم رگرسیون محلی مبتنی بر وزن
معایب الگوریتم رگرسیون محلی مبتنی بر وزن : LOESS نسبت به سایر روش های حداقل مربعات از کارآیی کمتری استفاده می کند. برای تولید مدل های خوب، نیاز به مجموعه داده های نسبتاً بزرگ و نمونه برداری متراکم دارد. این به این دلیل است که LOESS هنگام انجام محاسبات محلی به ساختار داده های محلی متکی است. بنابراین، LOESS تحلیل داده های پیچیده تری را در ازای هزینه های تجربی بیشتر ارائه می دهد. یکی دیگر از معایب LOESS این واقعیت است که یک تابع رگرسیون تولید نمی کند که به راحتی با یک فرمول ریاضی نشان داده می شود. این می تواند انتقال نتایج تجزیه و تحلیل را به افراد دیگر دشوار کند. برای انتقال توضیحات تابع رگرسیون به شخص دیگر، آن ها به مجموعه داده و نرم افزار برای محاسبات LOESS نیاز دارند.
در رگرسیون غیر خطی، از سوی دیگر، فقط نوشتن یک فرم کاربردی برای ارائه برآورد پارامترهای ناشناخته و عدم قطعیت برآورد شده ضروری است. بسته به کاربرد، این می تواند یک اشکال عمده در استفاده از LOESS باشد. به طور خاص، از فرم ساده LOESS نمی توان برای مدل سازی مکانیکی استفاده کرد که پارامترهای مجهز ویژگی های فیزیکی خاص یک سیستم را مشخص می کنند. سرانجام، همانطور که در بالا مورد بحث قرار گرفت ، LOESS یک روش محاسباتی فشرده است. LOESS نیز مانند سایر روش های حداقل مربعات مستعد تأثیرات داده های پرت در مجموعه داده قرار می گیرد.
جمع بندی الگوریتم رگرسیون محلی مبتنی بر وزن
جمع بندی الگوریتم رگرسیون محلی مبتنی بر وزن : الگوریتم رگرسیون با وزن محلی بسیار مهم و پرکاربرد است. این الگوریتم بیشتر برای زمانی استفاده می شود که داده ها دارای یک توزیع خطی نیستند. در انتخاب تابع های برازش باید کاملاً دقت کرد تا الگوریتم دچار بیش برازش نشود زیرا این مشکل باعث می شود که الگوریتم داده ها را حفظ کند و در داه های آموزش به خوبی بتواند خروجی را پیش بینی کند ولی در داده های آزمون بسیار ضعیف عمل کند.
نویسنده: تیم پژوهش راهبرد

 مقایسه روش های عمومی و رگرسیون با وزن محلی
مقایسه روش های عمومی و رگرسیون با وزن محلی 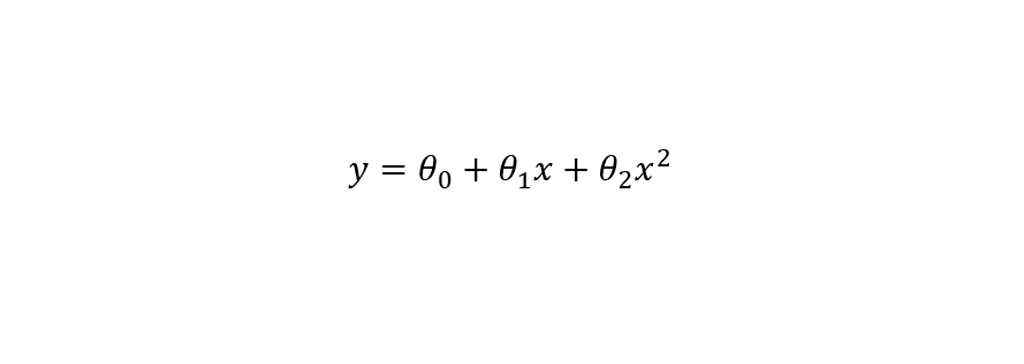
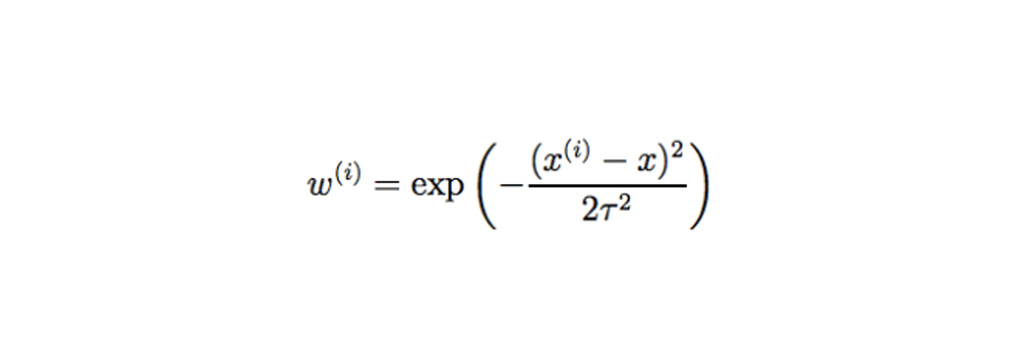 مزیت الگوریتم رگرسیون محلی مبتنی بر وزن
مزیت الگوریتم رگرسیون محلی مبتنی بر وزن



1 دیدگاه
ممنون از مقاله خوبتون.