خوشه بندی سلسله مراتبی (Hierarchical clustering)

مقدمه ای بر خوشه بندی سلسله مراتبی (Hierarchical clustering)

تکنیک خوشه بندی سلسله مراتبی (Hierarchical clustering) یکی از تکنیک های رایج خوشه بندی در یادگیری ماشین است. این الگوریتم در دسته الگوریتم های یادگیری بدون نظارت است و بسیار پر کاربرد است. قبل از اینکه بخواهیم مفهوم تکنیک خوشه بندی سلسله مراتبی را با هم بررسی کنیم، بهتر است در ابتدا مفهوم خوشه بندی را مرور کنیم.

خوشه بندی چیست ؟

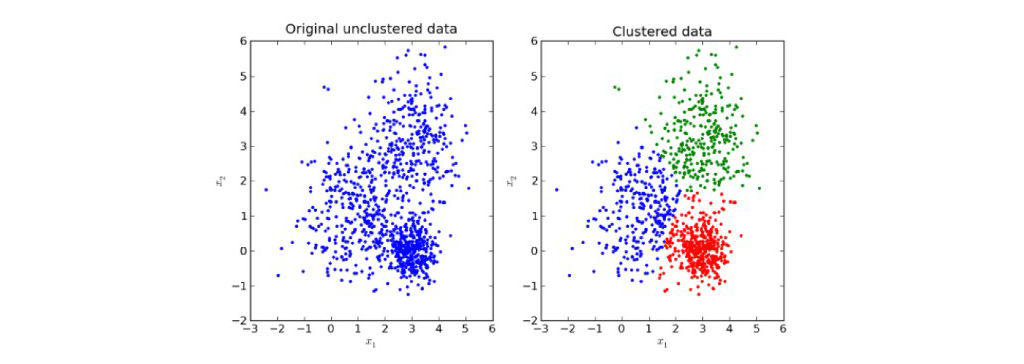
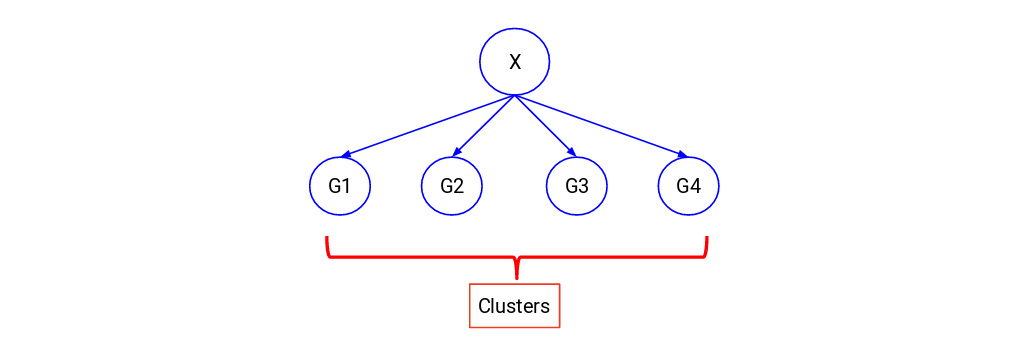
خوشه بندی اساساً تکنیکی است که نقاط داده مشابه را گروه بندی می کند به طوری که نقاط یک گروه بیشتر از نقاط دیگر گروه ها به یکدیگر شباهت دارند. گروه نقاط مشابه داده را Cluster می نامند.

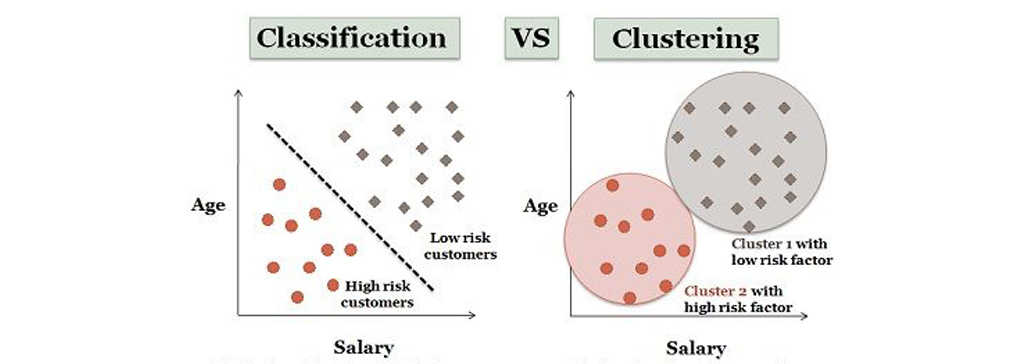
تفاوت بین مدل های خوشه بندی و طبقه بندی/رگرسیون:

در مدل های طبقه بندی و رگرسیون، یک مجموعه دیتا (D) به ما داده می شود که حاوی نقاط داده و برچسب های کلاس است. این مدل ها شامل یادگیری با نظارت است.

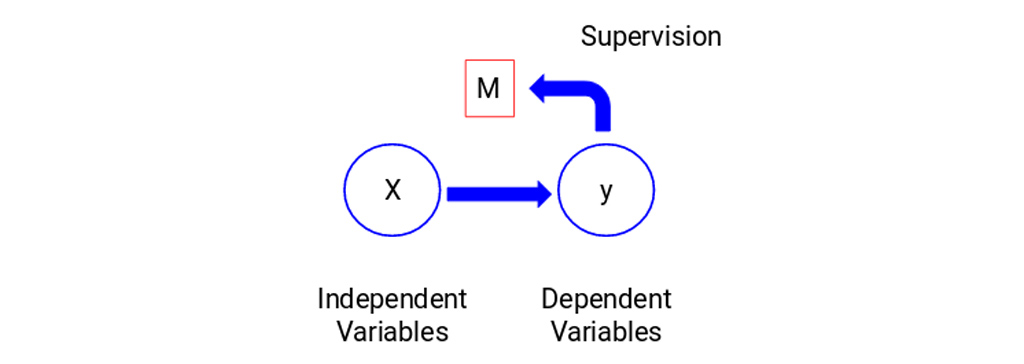
در اینجا، y متغیر وابسته یا هدف ما است و X نشان دهنده متغیرهای مستقل است. متغیر هدف به X وابسته است و بنابراین X متغیر وابسته نیز نامیده می شود. ما مدل خود را با استفاده از متغیرهای مستقل با نظارت بر متغیر هدف آموزش می دهیم و بنابراین نام آموزش، آموزش تحت نظارت است. هدف ما هنگام آموزش مدل، ایجاد تابعی است که متغیرهای مستقل را به هدف مورد نظر ترسیم کند. پس از آموزش مدل، می توانیم مجموعه جدیدی از مشاهدات را ارائه دهیم و تا مدل، هدف را برای آن ها پیش بینی کند. این، به طور خلاصه، یادگیری تحت نظارت است.

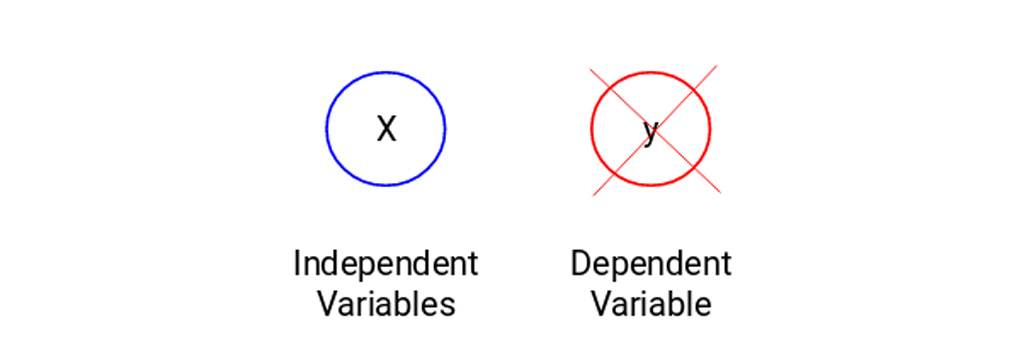
ممکن است شرایطی پیش بیاید که هیچ متغیری هدف برای پیش بینی نداشته باشیم. چنین مشکلاتی، بدون هیچ گونه متغیر هدف مشخص، به عنوان مسائل یادگیری بدون نظارت شناخته می شوند. در این نوع مسائل فقط متغیرهای مستقل داریم و هیچ متغیر هدف/وابسته ای در این مسائل نداریم.

ما سعی می کنیم در این موارد کل داده ها را به مجموعه ای از گروه ها تقسیم کنیم. این گروه ها به عنوان خوشه و فرآیند ساخت این خوشه ها به عنوان خوشه بندی شناخته می شوند. وقتی صحبت از خوشه بندی می شود، یک مجموعه داده در اختیار ما قرار می گیرد که فقط شامل نقاط داده (D) است. در اینجا برچسب های کلاس (D) به ما ارائه نشده است.

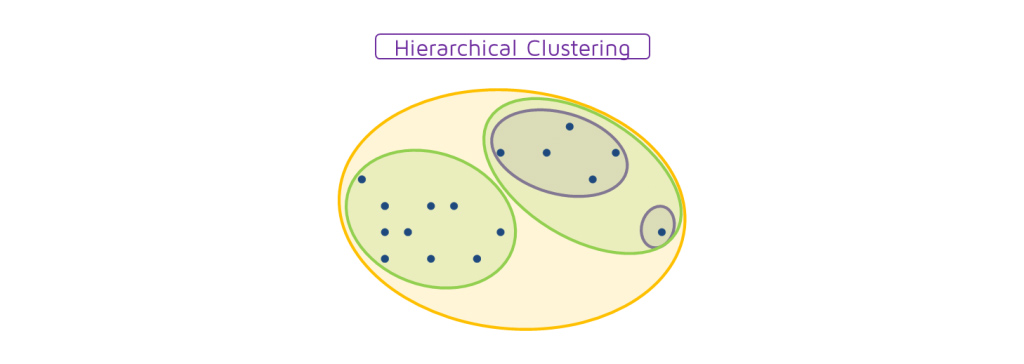
خوشه بندی سلسله مراتبی (Hierarchical clustering)

این تکنیک به طور کلی برای دسته بندی جمعیت در گروه های مختلف استفاده می شود. چند مثال رایج شامل تقسیم بندی مشتریان، دسته بندی اسناد مشابه با یکدیگر، توصیه آهنگ ها یا فیلم های مشابه و غیره است. برنامه های کاربردی بیشتری برای یادگیری بدون نظارت وجود دارد. در حال حاضر، الگوریتم های مختلفی وجود دارد که به ما در ساخت این خوشه ها کمک می کند. متداول ترین الگوریتم های خوشه بندی، K-means و خوشه بندی سلسله مراتبی هستند.

فرض کنید نقاط زیر را داریم و می خواهیم آن ها را در گروه ها مختلف دسته بندی کنیم. ما می توانیم هر یک از این نقاط را به یک خوشه جداگانه اختصاص دهیم:

اکنون ، بر اساس شباهت این خوشه ها، می توانیم شبیه ترین خوشه ها را با هم ترکیب کرده و این روند را تکرار کنیم تا تنها یک خوشه باقی بماند:

 

انواع مختلف خوشه بندی سلسله مراتبی

عمدتا دو نوع خوشه بندی سلسله مراتبی وجود دارد:

• Agglomerative hierarchical clustering: (روش پایین به بالا یا تجمعی)
• Divisive Hierarchical clustering: (روش بالا به پایین یا تقسیمی)

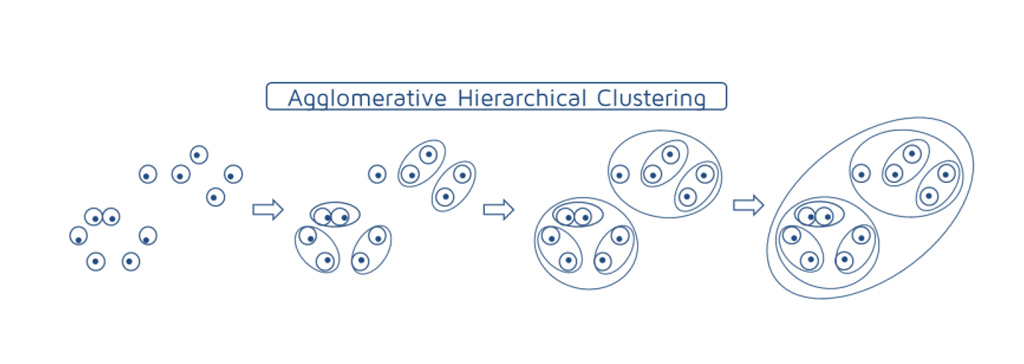
روش خوشه بندی از پایین به بالا (خوشه بندی تجمعی یا Agglomerative hierarchical clustering )

در این تکنیک هر نقطه را به یک خوشه خاص، اختصاص می دهد. فرض کنید 11 نقطه داده وجود دارد. هر یک از این نقاط را به یک خوشه اختصاص می دهد و بنابراین در ابتدا 11 خوشه خواهیم داشت. هر نقطه به یک خوشه اختصاص داده می شود. سپس، در هر تکرار، نزدیکترین جفت خوشه را ادغام می شود و این مرحله تکرار می شود تا نهایتاً یک خوشه باقی بماند. ادغام هر دو خوشه نزدیک به هم تا زمانی که فقط یک خوشه داشته باشیم. ما در هر مرحله خوشه ها را ادغام (یا اضافه) می کنیم. از این رو، این نوع خوشه بندی به عنوان خوشه بندی سلسله مراتبی افزایشی نیز شناخته می شود.

 

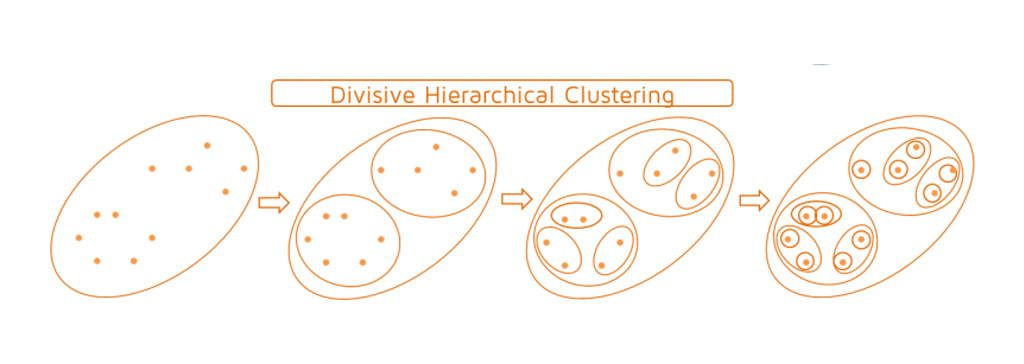
روش خوشه بندی از بالا به پایین (خوشه بندی تقسیمی یا Divisive Hierarchical clustering )

خوشه بندی سلسله مراتبی از بالا به پایین بر عکس عمل می کند. به جای شروع با n خوشه (در صورت n نقطه داده)، با یک خوشه شروع می کند و تمام نقاط را به آن خوشه اختصاص می دهد. بنابراین، مهم نیست که ما 10 یا 1000 نقطه داده داشته باشیم. همه این نقاط در ابتدا متعلق به یک خوشه هستند. اکنون، در هر تکرار، دورترین نقطه در خوشه را جدا می کند و این روند را تکرار می شود تا زمانی که هر خوشه فقط حاوی یک نقطه واحد باشد. در این روش خوشه ها در هر مرحله تقسیم می شود (splitting or dividing)، از این رو نام خوشه بندی سلسله مراتبی تقسیم کننده است.

بررسی الگوریتم خوشه بندی سلسله مراتبی به صورت گام به گام

ما شبیه ترین نقاط یا خوشه ها را در خوشه بندی سلسله مراتبی ادغام می کنیم. حال این سوال مطرح می شود که چگونه می توانیم تصمیم بگیریم که کدام نقاط مشابه هستند و کدام شباهت ندارند؟ این یکی از مهمترین سوالات در خوشه بندی است! در اینجا یکی از روش های محاسبه شباهت بررسی می شود- فاصله بین سانتریید های (مرکز) این خوشه ها را در نظر بگیرید. نقاطی که کمترین فاصله را دارند نقاط مشابه نامیده می شوند و ما می توانیم آن ها را ادغام کنیم. ما همچنین می توانیم از این به عنوان یک الگوریتم مبتنی بر فاصله یاد کنیم (زیرا ما فاصله بین خوشه ها را محاسبه می کنیم).

در اینجا یکی از روش های محاسبه شباهت وجود دارد – فاصله بین سانترییدهای این خوشه ها را در نظر بگیرید. نقاطی که کمترین فاصله را دارند نقاط مشابه هستند و  می توانیم آنها را ادغام کنیم. ما همچنین می توانیم از این به عنوان یک الگوریتم مبتنی بر فاصله یاد کنیم (زیرا ما فاصله بین خوشه ها را محاسبه می کنیم). در خوشه بندی سلسله مراتبی، مفهومی داریم به نام ماتریس مجاورت. این ماتریس فاصله بین هر نقطه را ذخیره می کند.

بیایید یک مثال برای درک این ماتریس و همچنین مراحل انجام خوشه بندی سلسله مراتبی ببینیم. فرض کنید یک معلم قصد دارد دانش آموزان خود را به گروه های مختلف تقسیم کند. او نمره هایی را دارد که هر دانش آموز در یک تکلیف بدست آورده است و بر اساس این نمرات، می خواهد آن ها را به گروه هایی تقسیم کند. در اینجا هیچ هدف ثابتی برای تعداد گروه ها وجود ندارد. از آنجا که معلم نمی داند چه نوع دانش آموزانی باید به کدام گروه اختصاص داده شود، نمی توان آن را به عنوان یک مشکل یادگیری تحت نظارت حل کرد. بنابراین، سعی می شود که خوشه بندی سلسله مراتبی را در اینجا اعمال شود و دانش آموزان را به گروه های مختلف تقسیم بندی کند.

بیایید یک نمونه از 5 دانش آموز بگیریم:

ایجاد ماتریس مجاورت

ابتدا، یک ماتریس مجاورت ایجاد می کنیم که فاصله بین هر یک از این نقاط را به ما می گوید. از آنجا که ما فاصله هر نقطه را از هر نقطه دیگر محاسبه می کنیم، یک ماتریس مربعی از شکل n * n که n تعداد مشاهدات  و فواصل بین نقاط را بدست می آوریم.

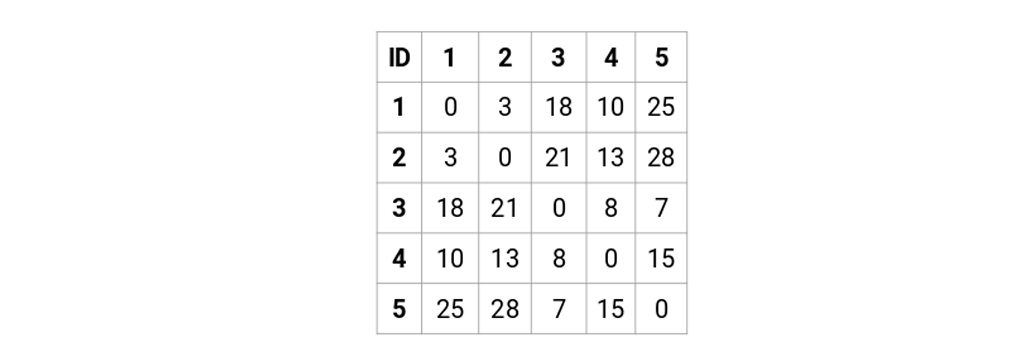
بیایید ماتریس مجاورت 5 * 5 را برای مثال خود بسازیم:

عناصر روی قطر اصلی این ماتریس همیشه صفر خواهد بود زیرا فاصله یک نقطه با خودش همیشه صفر است. ما از فرمول فاصله اقلیدسی برای محاسبه بقیه فاصله ها استفاده خواهیم کرد. بنابراین، فرض کنید می خواهیم فاصله بین نقطه 1 و 2 را محاسبه کنیم:

به طور مشابه، ما می توانیم تمام فاصله ها را محاسبه کرده و ماتریس مجاورت را پر کنیم.

مرحله 1: ابتدا ، تمام نقاط را به یک خوشه اختصاص می دهیم. هر رنگ نشان دهنده یک گروه است:

می بینید که ما 5 خوشه مختلف برای 5 نقطه در داده های خود داریم.

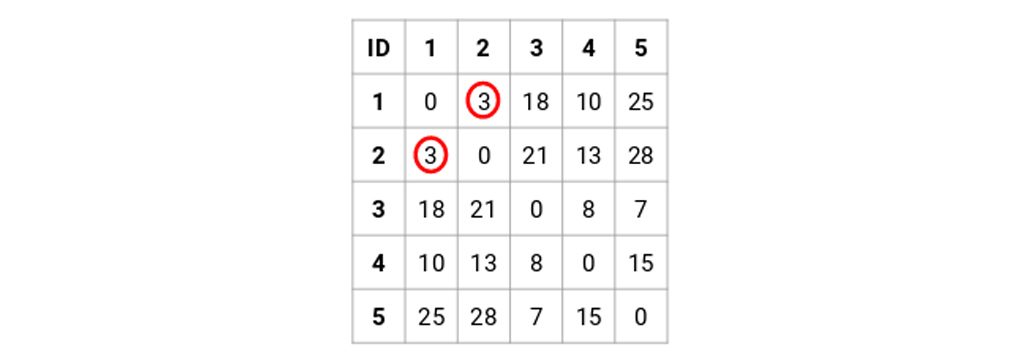
مرحله 2: بعد، ما کوچکترین فاصله را در ماتریس مجاورت پیدا کرده و نقاط را با کوچکترین فاصله ادغام می کنیم. سپس ماتریس مجاورت را به روز می کنیم:

در اینجا، کوچکترین فاصله 3 است و بنابراین نقطه 1 و 2 را ادغام می کنیم:

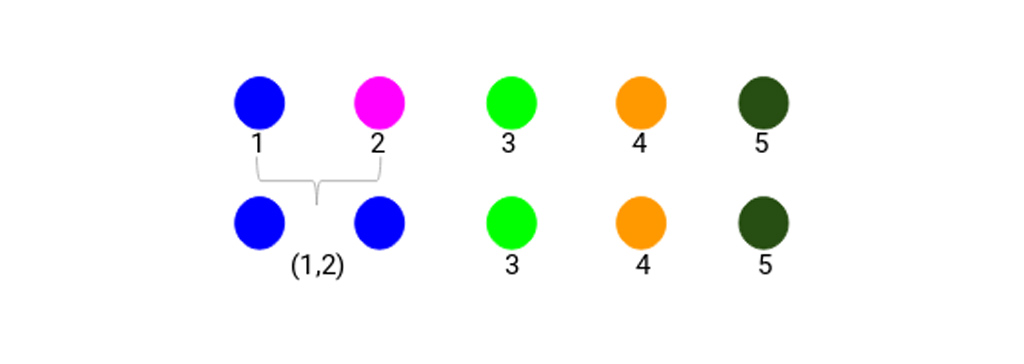
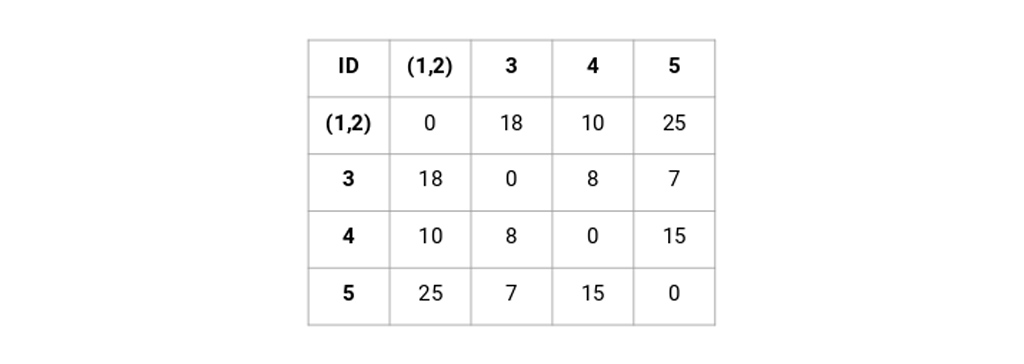
بیایید به خوشه های به روز شده نگاه کنیم و بر این اساس ماتریس مجاورت را به روز کنیم:

در اینجا، ما حداکثر دو نقطه (7 ، 10) را برای جایگزینی در این خوشه در نظر گرفته ایم. به جای حداکثر ما همچنین می توانیم حداقل مقدار یا مقادیر متوسط ​​را نیز در نظر بگیریم. اکنون، ما دوباره ماتریس مجاورت این خوشه ها را محاسبه می کنیم:

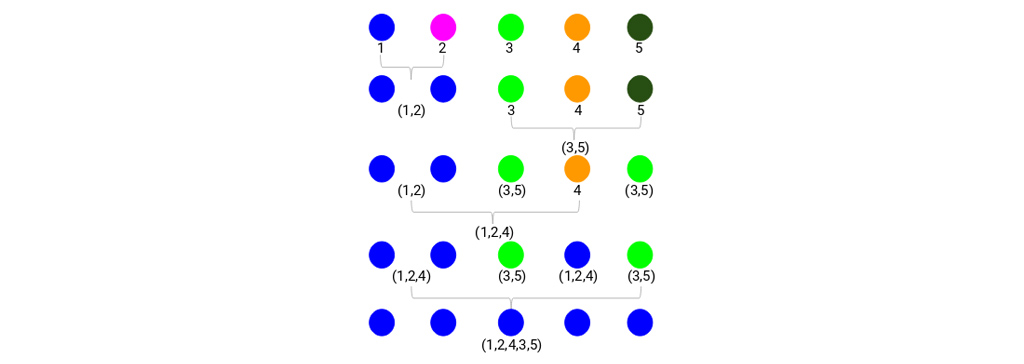
مرحله 3: مرحله 2 را تکرار می کنیم تا فقط یک خوشه باقی بماند.

ما با 5 خوشه شروع کردیم و در نهایت یک خوشه واحد داشتیم. این نحوه عملکرد خوشه بندی سلسله مراتبی تجمعی است. اما این سوال همچنان باقی است – چگونه تعداد خوشه ها را تعیین کنیم؟

چگونه باید تعداد خوشه ها را در خوشه بندی سلسله مراتبی انتخاب کنیم؟

برای بدست آوردن تعداد خوشه ها برای خوشه بندی سلسله مراتبی، ما از یک مفهوم عالی به نام Dendrogram استفاده می کنیم. دندروگرام یک نمودار درختی است که دنباله های ادغام شده یا تقسیم شده(بسته به نوع خوشه بندی) را ثبت می کند. به مثال معلم و دانش آموز توجه کنیم. هرگاه دو خوشه را ادغام کنیم، یک دندروگرام فاصله بین این خوشه ها را ثبت کرده و آن را به شکل نمودار نشان می دهد.

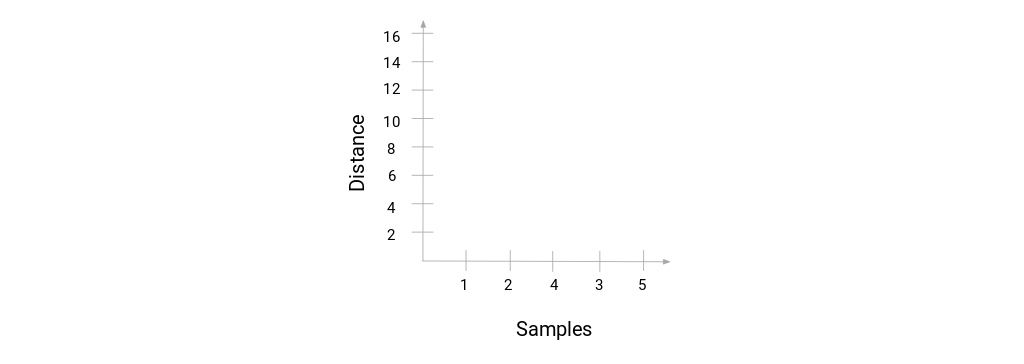
ما نمونه های مجموعه داده را در محور x و فاصله در محور y داریم. هرگاه دو خوشه ادغام شوند، ما در این دندروگرام آن ها را به هم وصل می کنیم و ارتفاع اتصال، فاصله بین این نقاط خواهد بود. بیایید دندروگرام را برای مثال خود بسازیم:

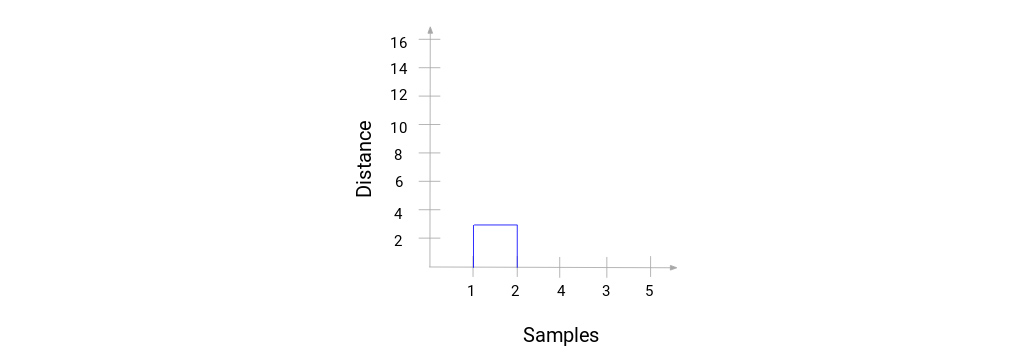
ما با ادغام نمونه 1 و 2 شروع کردیم و فاصله بین این دو نمونه 3 بود (به اولین ماتریس مجاورت در قسمت قبل مراجعه کنید). بیایید این را در دندروگرام ترسیم کنیم:

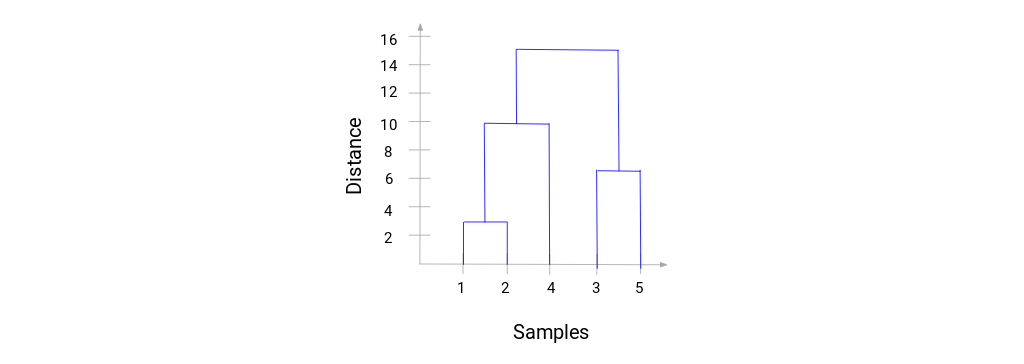
در اینجا می بینیم که نمونه 1 و 2 را ادغام کرده ایم. خط عمودی نشان دهنده فاصله بین این نمونه ها است. به طور مشابه، همه مراحل را در جایی که خوشه ها را ادغام کردیم ترسیم می کنیم و در نهایت، یک دندروگرام به این شکل دریافت می کنیم:

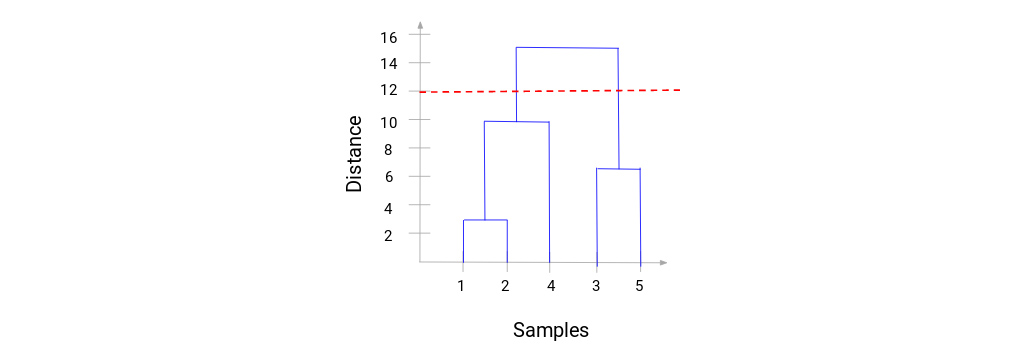
ما می توانیم مراحل خوشه بندی سلسله مراتبی را به وضوح تجسم کنیم. هر چه فاصله خطوط عمودی در دندروگرام بیشتر، فاصله بین آن دسته ها بیشتر است. اکنون، می توانیم فاصله آستانه را تعیین کرده و خط افقی بکشیم (به طور کلی، سعی می کنیم آستانه را به گونه ای تنظیم کنیم که بلندترین خط عمودی را قطع کند). بیایید این آستانه را 12 قرار دهیم و یک خط افقی ترسیم کنیم:

تعداد خوشه ها تعداد خطوط عمودی است که با خطی که با استفاده از آستانه کشیده شده است قطع می شوند. در مثال بالا، از آنجا که خط قرمز 2 خط عمودی را قطع می کند، 2 خوشه خواهیم داشت. یک خوشه دارای نمونه (1،2،4) و نمونه دیگر دارای نمونه (3،5) خواهد بود. کاملاً ساده است. به این ترتیب می توان تعداد خوشه ها را با استفاده از دندروگرام در خوشه بندی سلسله مراتبی تعیین کرد.

مزیت خوشه بندی سلسله مراتبی

1. درک و پیاده سازی این الگوریتم خوشه بندی سلسله مراتبی بسیار آسان است.
2. خروجی دندروگرام الگوریتم می تواند برای درک تصویر بزرگ و همچنین گروه های موجود در داده های شما استفاده شود.
3. نیازی به تعیین تعدادگروه ها از قبل ندارد.

نقاط ضعف خوشه بندی سلسله مراتبی

نقاط ضعف الگوریتم خوشه بندی سلسله مراتبی شامل موارد زیر است:

1. این الگوریتم به ندرت بهترین راه حل را ارائه می دهد.
2. نتایج این الگوریتم شامل بسیاری از تصمیمات دلخواه است.
3. برای داده های از دست رفته کاری نمی تواند انجام دهد.
4. این الگوریتم با انواع داده های ترکیبی ضعیف کار می کند.
5. روی مجموعه داده های بسیار بزرگ و خروجی اصلی آن جواب مناسبی نمی دهد

کاربرد های خوشه بندی سلسله مراتبی

1. گروه بندی کردن مشتریان یک فروشگاه بر اساس نظر یا سبد خرید و …..
2. گروه بندی کردن دانش آموزان یا دانشجویان
3. گروه بندی کردن بیماران و بررسی تاثیر دارو و میزان پیشرفت بیماری
4. پیشنهاد فیلم و موزیک و به طور کلی استفاده در سیستم های پیشنهاد دهی

جمع بندی خوشه بندی سلسله مراتبی (Hierarchical clustering)

در تجزیه و تحلیل داده ها، الگوریتم های خوشه بندی سلسله مراتبی ابزارهای قدرتمندی هستند که به شناسایی خوشه های طبیعی می پردازند، اغلب بدون هیچ گونه اطلاعات قبلی از ساختار داده ها مورد استفاده قرار می گیرند. زیرا نمای گرافیکی از پارتیشن های حاصله، سلسله مراتب یا دندروگرام را ارائه می دهد و اطلاعات بیشتری را آشکار می کند. علاوه بر این، نیازی به تعیین تعداد خوشه ها به صورت از قبل تعیین شده نیست. برش دندروگرام در سطوح مختلف در سلسله مراتب، پارتیشن های متفاوتی را ایجاد می کند و همچنین، استفاده از روش های مختلف تجمیع خوشه ها برای مجموعه داده های یکسان می تواند سلسله مراتب متفاوتی ایجاد کند و در نتیجه پارتیشن های متفاوتی ایجاد کند. الگوریتم خوشه بندی سلسله مراتبی برای شروع آموزش یکی از مهم ترین الگوریتم ها در تحلیل داده ها محسوب می شود.

 

منابع

www.analyticsvidhya.com

www.geeksforgeeks.org