بیز ساده گاوسی Gaussian Naive Bayes یا الگوریتم دسته بند بیز ساده
بیز ساده گاوسی Gaussian Naive Bayes یا الگوریتم دسته بند بیز ساده
بیز ساده گاوسی Gaussian Naive Bayes یا الگوریتم دسته بند بیز ساده : طبقه بندی کننده های ساده بیز بر اساس قضیه بیز ساخته شده اند. یکی از مفروضات این فرضیه استقلال بین ویژگی ها است. این طبقه بندی کننده ها فرض می کنند که ارزش یک ویژگی خاص مستقل از ارزش هر ویژگی دیگر است. در شرایط یادگیری تحت نظارت، طبقه بندی کننده های Naive Bayes بسیار کارآمد آموزش می بینند. طبقه بندی کننده های ساده برای برآورد پارامترهای مورد نیاز برای طبقه بندی به داده های آموزشی کمی نیاز دارند. طبقه بندی کننده های ساده Naive Bayes طراحی و پیاده سازی ساده ای دارند و می توانند در بسیاری از موقعیت های واقعی زندگی کاربرد داشته باشند.
الگوریتم دسته بند بیز ساده
قضیه بیز در یادگیری ماشین برای مبحث کلاسه بندی بسیار مورد استفاده قرار می گیرد. ما اغلب علاقمند به انتخاب بهترین فرضیه (h) برای داده های داده شده (d) هستیم. در یک مسئله طبقه بندی، فرضیه ما (h) ممکن است کلاسی باشد که برای یک نمونه داده جدید (d) تعیین می شود. یکی از ساده ترین روش های انتخاب محتمل ترین فرضیه با توجه به داده هایی که در اختیار داریم و می توانیم از آنها به عنوان دانش قبلی خود در مورد مسئله استفاده کنیم. قضیه بیز راهی را ارائه می دهد که با توجه به دانش قبلی خود می توان احتمال فرضیه را محاسبه کرد. قضیه بیز به شکل زیر بیان شده است.
P(h |d) = (P(d |h) * P(h)) / P(d)
جایی که P (h | d) احتمال فرضیه h با توجه به داده های d است. این احتمال، احتمال خلفی نامیده می شود. P (d | h) احتمال داده های d است که فرضیه h درست بوده است. P (h) احتمال درست بودن فرضیهh (صرف نظر از داده ها) است. این احتمال اولیه h نامیده می شود. P (d) احتمال داده ها (صرف نظر از فرضیه) است.
پس از محاسبه احتمال خلفی برای تعدادی از فرضیه های مختلف، می توانید فرضیه را با بیشترین احتمال انتخاب کنید. این حداکثر فرضیه محتمل است و ممکن است به طور رسمی فرضیه حداکثر خلفی (MAP) نامیده شود. این را می توان به صورت زیر نوشت:
MAP(h) = max(P(h |d))
or
MAP(h) = max((P(d |h) * P(h)) / P(d))
or
MAP(h) = max(P(d |h) * P(h))
P (d) یک اصطلاح نرمال سازی است که به ما امکان محاسبه احتمال را می دهد. زمانی می توانیم آن را کنار بگذاریم که به محتمل ترین فرضیه علاقه مند باشیم زیرا ثابت است و فقط برای نرمال سازی مورد استفاده قرار می گیرد. به مبحث طبقه بندی بر می گردیم، اگر در داده های آموزشی خود تعدادی نمونه در هر کلاس داشته باشیم، احتمال هر کلاس به عنوان مثال برابر P(h) خواهد بود. باز هم، این یک عبارت ثابت در معادله ما خواهد بود و می توانیم آن را کنار بگذاریم تا به نتیجه برسیم.
MAP(h) = max(P(d |h))
طبقه بندی کننده بیز ساده
طبقه بندی کننده بیز ساده : Naive Bayes یک الگوریتم طبقه بندی برای مشکلات طبقه بندی دوتایی و چند تایی است. درک آسان این تکنیک زمانی است که با استفاده از مقادیر ورودی باینری یا دسته ای توصیف می شود. به این بیز ساده گفته می شود. زیرا محاسبه احتمالات برای هر فرضیه ساده شده است تا محاسبه آنها قابل پذیرش باشد. به جای تلاش برای محاسبه مقادیر هر ویژگیP(d1, d2, d3|h) ، با توجه به مقدار مورد نظر هر کدام از داده ها را به صورت شرطی مستقل بررسی می شود و به صورت P (d1 | h) * P (d2 | H) محاسبه می شود. این یک فرض بسیار کامل است که در داده های واقعی بسیار بعید به نظر می رسد، یعنی این که احتمال آن خیلی کم است که ویژگی ها برهم کنش نداشته باشند. با این وجود، این رویکرد در مورد داده هایی که شامل این فرضیه نمی شود به طرز شگفت آوری خوب عمل می کند.
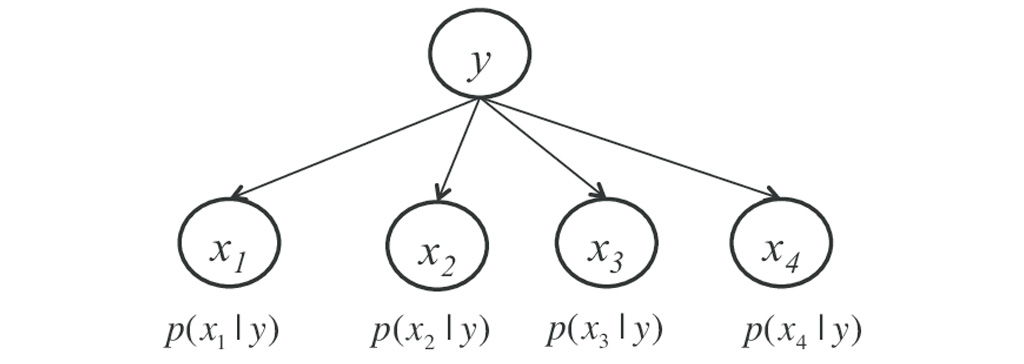
مدل های بیز ساده
مدل بیز ساده شامل احتمالات زیر است.
احتمالات کلاس: احتمالات هر کلاس در مجموعه داده آموزش.
احتمالات شرطی: احتمالات مشروط هر مقدار ورودی با توجه به هر مقدار کلاس.
مدل ساده بیز توسط داده ها آموزش می بیند و یادگیری مدل بیز ساده از داده های آموزشی سریع است. آموزش سریع است زیرا فقط احتمال هر کلاس محاسبه می شود و احتمال هر کلاس با توجه به مقادیر مختلف ورودی (x) باید محاسبه شود. نیازی نیست ضرایبی با روش های بهینه سازی تنظیم شوند.
مثال الگوریتم دسته بند بیز ساده
محاسبه احتمالات کلاس
احتمالات کلاس به این صورت محاسبه می شود که فراوانی نمونه (تعداد نمونه) در هر کلاس تقسیم می شود بر تعداد کل نمونه ها. به عنوان مثال در طبقه بندی باینری، احتمال وجود نمونه ای متعلق به کلاس 1 به صورت زیر محاسبه می شود:
P(class=1) = count(class=1) / (count(class=0) + count(class=1))
در ساده ترین حالت، هر کلاس دارای احتمال 0.5 یا 50 درصد برای هر مسئله طبقه بندی باینری با تعداد نمونه مشابه در هر کلاس است.
محاسبه احتمالات شرطی
احتمالات مشروط به این روش محاسبه می شوند که فراوانی هر مقدار از ویژگی برای یک کلاس معین تقسیم بر فراوانی نمونه ها در آن کلاس است. به عنوان مثال، اگر یک ویژگی ” weather” دارای مقادیر ” sunny” و ” rainy ” و ویژگی کلاس دارای مقادیر کلاس ” go-out” و ” stay-home” است، پس احتمالات مشروط هر مقدار weather برای هر کلاس را می توان به صورت زیر محاسبه کرد:
P(weather = sunny | class = go-out) = count(instances with weather = sunny and class = go-out) / count(instances with class = go-out)
P(weather = sunny | class = stay-home) = count(instances with weather = sunny and class = stay-home) / count(instances with class=stay-home)
P(weather = rainy |class=go-out) = count(instances with weather=rainy and class=go-out) / count(instances with class=go-out)
P(weather = rainy |class=stay-home) = count(instances with weather=rainy and class = stay-home) / count(instances with class=stay-home)
در مثال بالا (مثال الگوریتم دسته بند بیز ساده) می خواهیم احتمال بیرون رفتن از خانه یا ماندن در خانه را با در نظر گرفتن شرایط آب و هوایی بررسی کنیم. دو وضعیت آفتابی و بارانی داریم. احتمال را برای هر دو وضعیت و هر دو کلاس محاسبه می کنیم. یعنی احتمال بیرون رفتن با شرط این که هوا آفتابی باشد، در این جا کلاس بیرن رفتن است و در قسمت بعد احتمال ماندن در خانه با شرط آفتابی بودن هوا بررسی می شود در این جا کلاس مورد بررسی ماندن در خانه است. مرحله بعد بیرون رفتن با شرط بارانی بودن هوا است و کلاس مد نظر بیرون رفتن است. در قسمت بعد کلاس مد نظر ماندن در خانه است با شرط بارانی بودن هوا است.
با یک مدل بیز ساده می توان احتمالات را پیش بینی کرد با توجه به مدل بیز ساده، می توانید با استفاده از قضیه بیز برای داده های جدید هم پیش بینی کنید.
MAP(h) = max(P(d | h) * P(h))
با استفاده از مثال بالا، اگر نمونه جدیدی از آب و هوای آفتابی داشتیم، می توانیم محاسبه کنیم:
go-out = P(weather = sunny | class=go-out) * P(class=go-out)
stay-home = P(weather=sunny |class=stay-home) * P(class=stay-home)
ما می توانیم کلاسی را انتخاب کنیم که بیشترین مقدار محاسبه شده را داشته باشد. با نرمال سازی این مقادیر به صورت زیر می توان این مقادیر را به احتمال تبدیل کرد:
P (go-out |weather=sunny) = go-out / (go-out + stay-home)
P (stay-home |weather=sunny) = stay-home / (go-out + stay-home)
اگر متغیرهای ورودی بیشتری داشتیم می توانیم مثال بالا را بسط دهیم. به عنوان مثال، وانمود کنید که یک ویژگی ” car” با مقادیر ” working” و ” broken” داریم. ما می توانیم این احتمال را در معادله ضرب کنیم. به عنوان مثال در زیر محاسبه برچسب کلاس “” go-out با افزودن متغیر ورودی ” car” تنظیم می شود.
go-out = P (weather=sunny |class=go-out) * P (car=working |class=go-out) * P(class=go-out)
بیز ساده گاوسی Gaussian Naive Bayes
بیز ساده گاوسی Gaussian Naive Bayes : هنگام کار با داده های پیوسته، اغلب فرض بر این است که مقادیر پیوسته مربوط به هر کلاس بر اساس یک توزیع نرمال (یا گوسی) توزیع می شود. فرض بر این است که ویژگی ها عبارتند از داده خای مستقلی که احتمال آن طبق فرمول زیر محاسبه می شود:
بیز ساده گاوسی Gaussian Naive Bayes از ویژگی ها و مدل های ارزشمند پیوسته ای پشتیبانی می کند که هر یک مطابق با توزیع گوسی (معمولی) هستند. یک رویکرد برای ایجاد یک مدل ساده این است که فرض کنیم داده ها با توزیع گوسی بدون هیچ واریانس (ابعاد مستقل) بین ابعاد توصیف می شوند. این مدل را می توان به سادگی با یافتن میانگین و انحراف از معیار نقاط درون هر برچسب، که تنها چیزی است که برای تعریف چنین توزیعی مورد نیاز است ، مناسب دانست.
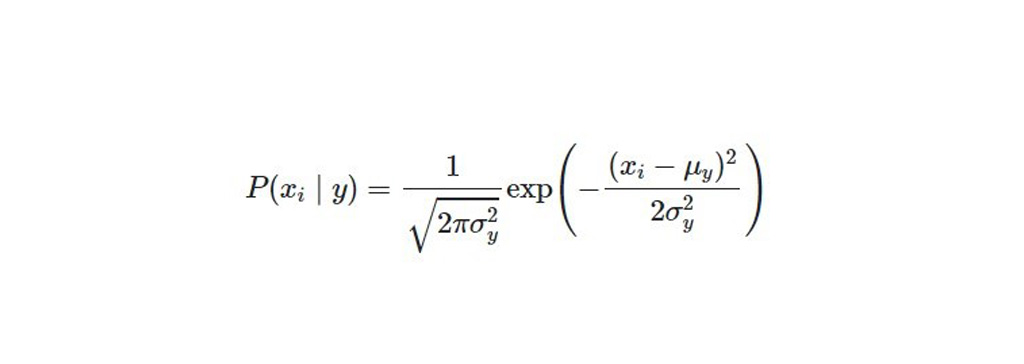
قضیه ی بیز را می توان به ویژگی هایی که ارزش واقعی دارند، عمدتا با فرض توزیع گوسی، گسترش داد. این توسعه بیز ساده را مدل بیز ساده گاوسی می نامند. برای برآورد توزیع داده ها می توان از توابع دیگر استفاده کرد، اما کار با توزیع گوسی (یا توزیع نرمال) ساده ترین کار است. زیرا شما فقط باید میانگین و انحراف استاندارد از داده های آموزشی خود را تخمین بزنید.
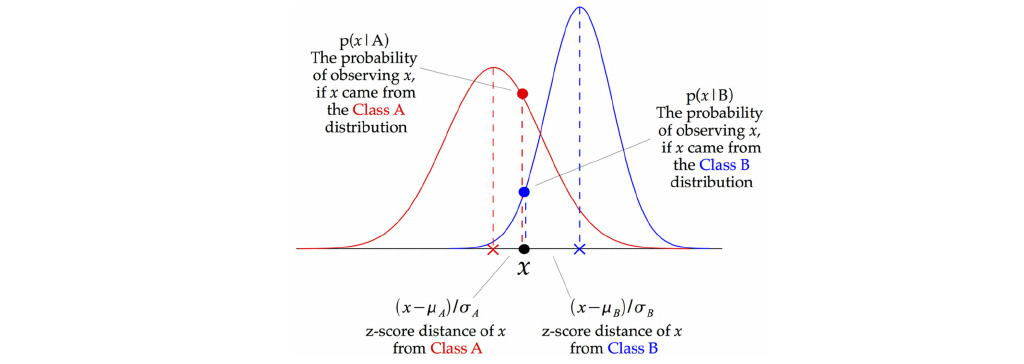
تصویر بالا نشان می دهد که چگونه طبقه بندی کننده Gaussian Naive Bayes (GNB) طبقه بندی می شود. در هر نقطه داده، فاصله نمره z بین آن نقطه و هر میانگین کلاس محاسبه می شود، یعنی فاصله از میانگین کلاس تقسیم بر انحراف از معیار آن کلاس. بنابراین، ما می بینیم که الگوریتم بیز ساده گاوسی رویکرد کمی متفاوتی دارد و می توان از آن به طور موثر استفاده کرد.
در مدل بیز ساده گاوسی Gaussian Naive Bayes احتمالات برای مقادیر ورودی و برای هر کلاس را با استفاده از یک فرکانس محاسبه کردیم. با ورودی هایی با ارزش واقعی، می توانیم میانگین و انحراف از معیار مقادیر ورودی (x) را برای هر کلاس محاسبه کنیم تا توزیع را خلاصه کنیم. این بدان معناست که علاوه بر احتمالات برای هر کلاس، ما همچنین باید میانگین و انحراف از معیار را برای هر متغیر ورودی برای هر کلاس ذخیره کنیم.
یک مدل ساده بیز گاوسی از داده های آموزشی، یاد می گیرد. این امر به سادگی محاسبه مقادیر میانگین و انحراف از معیار هر متغیر ورودی برای هر مقدار کلاس است.
mean(x) = 1/n * sum(x)
جایی که n تعداد نمونه ها و x مقادیر یک متغیر ورودی در داده های آموزشی است. با استفاده از معادله زیر می توان انحراف معیار را محاسبه کرد:
standard deviation(x) = sqrt (1/n * sum(xi-mean(x) ^ 2 ))
این ریشه دوم، مربع تفاوت هر مقدار x از مقدار میانگین x ها است. n تعداد نمونه است،sqrt() تابع ریشه دوم،sum () تابع مجموع، xi یک مقدار خاص متغیر x برای نمونه اول و میانگین داده های موجود است.
با استفاده از یک مدل بیز ساده گاوسی احتمالات مقادیر x جدید را با استفاده از تابع چگالی احتمال گاوسی محاسبه می شود.
(PDF) Probability Density Function
pdf(x, mean, sd) = (1 / (sqrt(2 * PI) * sd)) * exp(-((x-mean^2)/(2*sd^2)))
در صورتی که داده های ما توزیع گوسی داشته باشد می توان از این فرمول برای طبقه بندی آن استفاده کرد و با دقت بالا می توان داده ها را دسته بندی کرد.
go-out = P(pdf(weather)|class=go-out) * P(pdf(car)|class=go-out) * P(class=go-out)
آماده سازی داده های برای الگوریتم Naive Bayes
ورودی های دسته ای(Categorical Inputs): Naive Bayes دارای ویژگی های برچسب مانند دوتایی، دسته ای یا اسمی است.
ورودی های گاوسی(Gaussian Inputs): اگر متغیرهای ورودی دارای ارزش واقعی باشند، توزیع گوسی فرض می شود. در این صورت اگر توزیع متغیرهای داده ها، گوسی یا نزدیک به گاوسی باشد، الگوریتم بهتر عمل می کند. این ممکن است نیازمند این باشد که نقاط داده پرت را حذف کنیم.
مسائل طبقه بندی: Naive Bayes یک الگوریتم طبقه بندی مناسب برای طبقه بندی باینری و چند کلاسی است. از این الگوریتم می توان در این مسائل استفاده کرد و نتایج بسیار عالی دریافت کرد.
جمع بندی بیز ساده گاوسی Gaussian Naive Bayes یا الگوریتم دسته بند بیز ساده
بیز ساده گاوسی Gaussian Naive Bayes یا الگوریتم دسته بند بیز ساده : مدل بیز ساده دارای مدل های توسعه یافته ای است که آن ها نیز خروجی بسیار عالی دارند و با درصد صحت بالا می توانند داده ها را طبقه بندی کنند. این مدل برای داده های پیوسته با توزیع نرمال به کار می رود و تقریباض تاثیر ویزگی ها بر روی یک دیگر در این مدل در نظر گرفته نمی شود. مدل بیز یک مدل یادگیر بسیار قوی است و برای مسائل دنیای واقعی بسیار کاربرد دارد.
نویسنده: تیم پژوهش راهبرد
دیدگاهتان را بنویسید