الگوریتم درختان طبقه بندی و رگرسیون (CART)
سرفصل مطالب
الگوریتم درختان طبقه بندی و رگرسیون (CART)
Classification And Regression Trees
یادگیری ماشین یکی از پرطرف دارترین موضوعات مورد مطالعه در زمینه هوش مصنوعی بوده است. الگوریتم های زیادی تحت یادگیری ماشین وجود دارد که به دلیل ماهیت شفاف خود به طور خاص محبوبیت یافته اند. یکی از آنها الگوریتم درخت تصمیم است که در بین مردم به عنوان الگوریتم درختان طبقه بندی و رگرسیون (CART) شناخته می شود.
الگوریتم CART
الگوریتم CART نوعی الگوریتم طبقه بندی است که برای ساخت درخت تصمیم بر اساس شاخص ناخالصی جینی مورد نیاز است. این یک الگوریتم اساسی یادگیری ماشین است و طیف گسترده ای از موارد استفاده را ارائه می دهد. یک متخصص آمار به نام لئو بریمن این عبارت را برای توصیف الگوریتم های درخت تصمیم که ممکن است برای طبقه بندی یا مدل سازی مدل های پیش بینی رگرسیون استفاده شود، ابداع کرد. یک درخت است که به انواع زیر درخت تصمیم گیری اشاره می کند:
درخت طبقه بندی:
وقتی متغیر هدف پیوسته اس ، از درخت برای یافتن “طبقه” ای استفاده می شود که متغیر هدف به احتمال زیاد در آن قرار می گیرد.
درخت رگرسیون:
از این درختان برای پیش بینی مقدار یک متغیر پیوسته استفاده می شود. در این مطلب، درختان تصمیم گیری، الگوریتم CART و مدل های مختلف آن و مزایای الگوریتم CART را مورد بحث قرار می دهیم.
الگوریتم درخت تصمیم گیری:
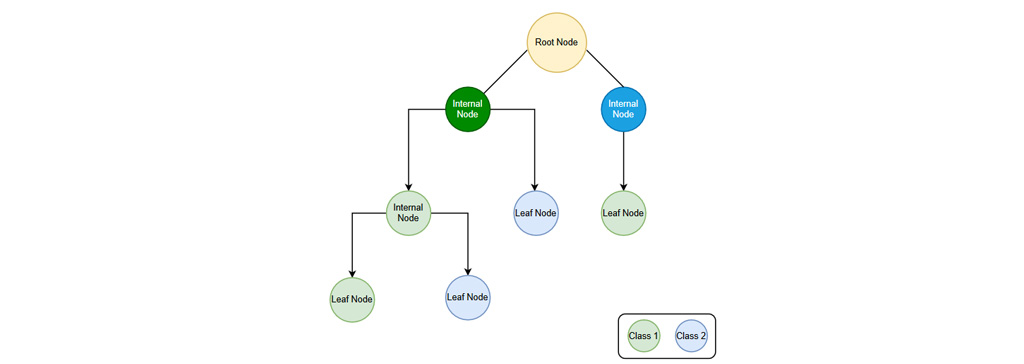
درخت تصمیم یک تکنیک است که برای تجزیه و تحلیل پیش بینی در زمینه های آمار، داده کاوی و یادگیری ماشین استفاده می شود. مدل پیش بینی در اینجا درخت تصمیم است و برای پیشرفت از مشاهدات در مورد نمونه هایی که توسط شاخه ها نشان داده می شود و در نهایت با مقدار هدف مورد نظر که در برگ ها نشان داده شده است، نتیجه گیری می شود. درختان تصمیم به دلیل خوانایی و سادگی، یکی از محبوب ترین روش های یادگیری ماشین هستند. ساختار یک درخت تصمیم از سه بخش اصلی تشکیل شده است: گره ها ریشه، گره های داخلی و گره های برگ
همانطور که در نمودار نشان داده شده است، اولین گره یا گره ریشه مجموعه داده های آموزشی است و بعد از آن گره داخلی و گره برگ. گره داخلی به عنوان گره تصمیم گیری عمل می کند، زیرا این نقطه ای است که در آن گره بر اساس بهترین ویژگی زیر گروه تقسیم می شود. گره نهایی یا گره برگ است که تصمیم را مشخص می کند.
الگوریتم CART در درخت تصمیم، گره ها بر اساس مقدار آستانه یک ویژگی به زیر گره ها تقسیم می شوند. الگوریتم CART این کار را با جستجوی بهترین همگن برای زیر گره ها، با کمک معیار شاخص جینی انجام می دهد. گره ریشه به عنوان مجموعه آموزشی در نظر گرفته می شود و با در نظر گرفتن بهترین ویژگی و مقدار آستانه به دو قسمت تقسیم می شود. علاوه بر این، زیر مجموعه ها نیز با استفاده از همان منطق تقسیم می شوند. این کار ادامه می یابد تا آخرین زیر مجموعه خالص در درخت یا حداکثر تعداد برگ ممکن در آن درخت در حال رشد یافت شود. این به هرس درخت نیز معروف است.
محاسبه شاخص جینی:
 مدل های الگوریتم CART برای داده
مدل های الگوریتم CART برای داده
مدل های الگوریتم CART برای داده : با توجه به مهارت یادگیری ماشین، مدل های CART با انتخاب متغیرهای ورودی و ارزیابی نقاط تقسیم بر روی آن متغیرها تا زمان ایجاد درخت مناسب شکل می گیرد. اجازه دهید مراحل مورد نیاز برای ایجاد درخت تصمیم با استفاده از الگوریتم CART را بررسی کنیم:
الگوریتم حریصانه
متغیرهای ورودی و نقاط تقسیم از طریق الگوریتم حریص انتخاب می شوند. ساخت درخت تصمیم باینری یک تکنیک تقسیم فضای ورودی است. یک حالت پایان از پیش تعیین شده، مانند حداقل تعداد نمونه های آموزشی که به هر گره برگ درخت داده شده است، برای متوقف ساختن درخت استفاده می شود. فضای ورودی با استفاده از روش حریص تقسیم می شود. این به عنوان تقسیم دوتایی بازگشتی شناخته می شود. این یک روش عددی است که در آن همه مقادیر در یک راستا قرار می گیرند و چندین نقطه تقسیم با استفاده از تابع هزینه آزمایش و ارزیابی می شوند و تقسیم با کمترین هزینه انتخاب می شود. تابع هزینه که برای تعیین نقاط تقسیم شده برای مشکلات مدل سازی پیش بینی رگرسیون کاهش می یابد، خطای مجموع مربع در تمام نمونه های آموزشی است که در زیر قرار دارد:
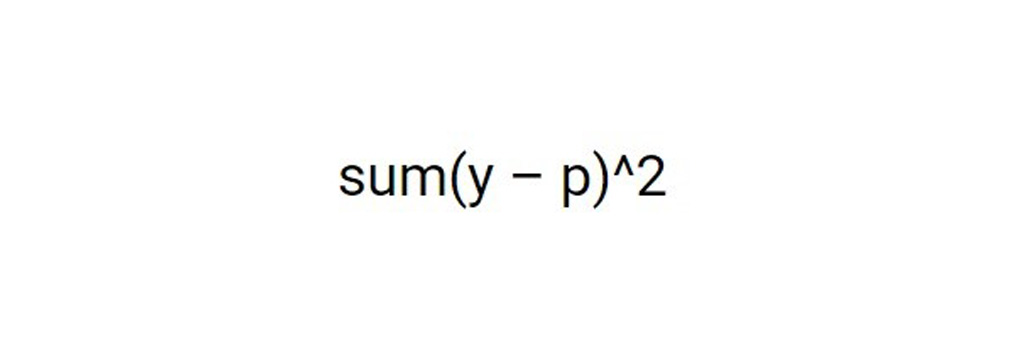
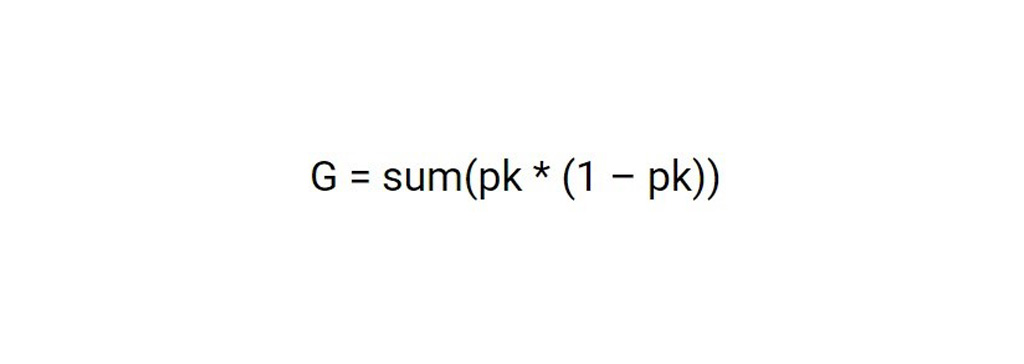
معیار توقف:
همانطور که با استفاده از داده های آموزشی روی درخت کار می کند، روش تقسیم دوتایی بازگشتی که در بالا توضیح داده شد باید بداند که چه موقع تقسیم را متوقف کند. متداول ترین روش توقف استفاده از حداقل مقدار داده آموزشی است که به هر گره برگ اختصاص داده شده است. اگر شمارش کمتر از یک آستانه مشخص باشد، تقسیم رد می شود و گره آخرین گره برگ محسوب می شود.
تعداد اعضای آموزش با توجه به مجموعه داده تنظیم می شود. مشخص می کند که داده های آموزشی در درخت چقدر باشد. به طور رایج و استاندارد معمولاً 70 درصد داده را جزو داده های آموزشی در نظر می گیرند و 30 درصد داده ها را جزو داده های آزمون در نظر می گیرند.
هرس درخت:
پیچیدگی درخت تصمیم به تعداد شکاف های درخت تعریف می شود. درختان با شاخه های کمتر بیشتر توصیه می شود. درک آنها ساده است و کمتر مستعد Over fit هستند. کار بر روی هر گره برگ در درخت و ارزیابی اثر حذف آن با استفاده از یک مجموعه آزمایش نگهدارنده، سریعترین و ساده ترین روش هرس است. اگر تابع هزینه کل مجموعه آزمایشی کامل کاهش یابد، فقط گره های برگ حذف می شوند. هنگامی که هیچ پیشرفت اضافی قابل دستیابی نیست، دیگر گره ها نباید حذف شوند.
روش های هرس پیشرفته تری، مانند هرس پیچیدگی هزینه (که به عنوان هرس ضعیف ترین پیوند نیز شناخته می شود)، قابل استفاده است، که در آن از پارامتر یادگیری (آلفا) برای تعیین اینکه آیا می توان گره ها را بسته به اندازه درخت فرعی حذف کرد، استفاده می شود.
آماده سازی داده ها برای الگوریتم CART: آماده سازی خاصی برای داده های الگوریتم CART مورد نیاز نیست.
الگوریتم درختان طبقه بندی و رگرسیون (CART) یک درخت باینری است. با عبور از درخت دوتایی با ثبت یک ورودی جدید، پیش بینی ها با CART انجام می شود. درخت با استفاده از الگوریتم حریصانه بر روی داده های آموزش برای انتخاب شکاف در درخت آموخته می شود. معیارهای توقف میزان یادگیری درخت را مشخص می کند و از هرس می توان برای بهبود درخت آموزش استفاده کرد.
مزایای الگوریتم درختان طبقه بندی و رگرسیون (CART)
از مزایای الگوریتم درختان طبقه بندی و رگرسیون (CART) میتوان به موارد زیر اشاره کرد:
- الگوریتم CART غیر پارامتری است، بنابراین به اطلاعات مربوط به نوع خاصی از توزیع بستگی ندارد.
- الگوریتم CART هر دو آزمایش را با مجموعه داده های آزمایش و اعتبار سنجی متقابل ترکیب می کند تا میزان تناسب را با دقت بیشتری اندازه گیری کند.
- CART به کاربر این امکان را می دهد که چندین بار از متغیرهای یکسان در مناطق مختلف درخت استفاده کند. این مهارت قادر است وابستگی متقابل پیچیدگی بین گروه های متغیر را آشکار کند.
- داده های پرت در متغیرهای ورودی تأثیر معنی داری بر CART ندارند.
- می توان محدودیت های توقف را لغو کرد تا درختان تصمیم گیری بیش از حد رشد کنند و سپس درخت را به اندازه ایده آل خود برش دهند. این روش با از توقف زود هنگام، احتمال از دست رفتن ساختار اساسی در مجموعه داده ها را کاهش می دهد. برای انتخاب مجموعه ورودی متغیرها، می توان از CART در ترکیب با سایر الگوریتم های پیش بینی استفاده کرد.
- الگوریتم CART می توانند بسیار مقاوم باشند. یک تغییر کوچک در داده های آموزش می تواند منجر به تغییر بزرگی در درخت و در نتیجه پیش بینی های نهایی شود.
معایب الگوریتم درختان طبقه بندی و رگرسیون (CART)
معایب الگوریتم درختان طبقه بندی و رگرسیون (CART) : یادگیری درخت تصمیم در چندین جنبه بهینه و حتی برای مفاهیم ساده ممکن است به صورت مسائل NP- کامل باشد. در نتیجه، الگوریتم های یادگیری درخت تصمیم مبتنی بر روش های ابتکاری مانند الگوریتم حریصانه است که در آن تصمیمات بهینه محلی در هر گره گرفته می شود راه گشای این مشکل است.
درختان تصمیم مشکل Over fit و Under fit می شوند.
عمق متوسط درخت که با تعداد گره ها یا آزمایش ها تا زمانی که طبقه بندی مشخص می شود، مطابق با معیارهای مختلف تقسیم بسیار زمان گیر است.
کاربرد الگوریتم CART
از کاربرد الگوریتم CART میتوان به موارد زیر اشاره کرد:
- ارزیابی فرصت های رشد در آینده: یکی از کاربردهای درخت تصمیم که شامل ارزیابی فرصت های رشد آینده برای مشاغل بر اساس داده های تاریخی است. از داده های تاریخی در مورد فروش می توان در درختان تصمیم گیری استفاده کرد که ممکن است منجر به ایجاد تغییرات اساسی در استراتژی یک کسب و کار برای کمک به توسعه و رشد شود.
- استفاده از داده های جمعیت شناختی برای یافتن مشتریان احتمالی: یکی دیگر از کاربردهای درخت تصمیم گیری استفاده از داده های جمعیت شناختی برای یافتن مشتریان احتمالی است. آن ها می توانند به ساده سازی بودجه بازاریابی و تصمیم گیری آگاهانه در مورد بازار هدف که تجارت بر آن متمرکز است، کمک کنند. در غیاب درختان تصمیم گیری، تجارت ممکن است بازار، بازاریابی خود را بدون در نظر گرفتن مشخصات جمعیتی خاص صرف کند، که بر درآمد کلی آن تأثیر می گذارد.
- خدمت به عنوان یک ابزار پشتیبانی در زمینه های مختلف: وام دهندگان همچنین از درخت تصمیم گیری برای پیش بینی احتمال عدم پرداخت مشتری به وام با استفاده از مدل پیش بینی مدل با استفاده از داده های قبلی مشتری استفاده می کنند. استفاده از ابزار پشتیبانی درخت تصمیم می تواند به وام دهندگان کمک کند تا میزان اعتبار مشتری را برای جلوگیری از ضرر ارزیابی کنند.
- استفاده از درخت تصمیم در تحقیقات: درخت تصمیم گیری همچنین می تواند در تحقیقات عملیاتی در برنامه ریزی لجستیک و مدیریت استراتژیک استفاده شود. آن ها می توانند در تعیین استراتژی های مناسب به شرکت کمک کنند تا به اهداف مورد نظر خود برسد. سایر زمینه هایی که می توان درختان تصمیم گیری را در آن به کار گرفت عبارتند از: مهندسی، آموزش، حقوق، تجارت، مراقبت های بهداشتی و … است.
نتیجه الگوریتم درختان طبقه بندی و رگرسیون (CART)
الگوریتم درختان طبقه بندی و رگرسیون (CART) زیر بخش Random Forest است که یکی از قوی ترین الگوریتم های یادگیری ماشین است. الگوریتم CART به عنوان مجموعه ای از داده هایی است که بر اساس ویژگی هایشان سازمان دهی می شود.. این الگوریتم به طور گسترده ای در تصمیم گیری درختان از طریق طبقه بندی و رگرسیون استفاده می شود. درختان تصمیم به طور گسترده ای در داده کاوی برای ایجاد مدلی که ارزش یک هدف را بر اساس مقادیر بسیاری از متغیرهای ورودی (یا متغیرهای مستقل) پیش بینی می کند، استفاده می شود.
نویسنده: تیم پژوهش راهبرد
منابع
www.hindawi.com/journals

 مدل های الگوریتم CART برای داده
مدل های الگوریتم CART برای داده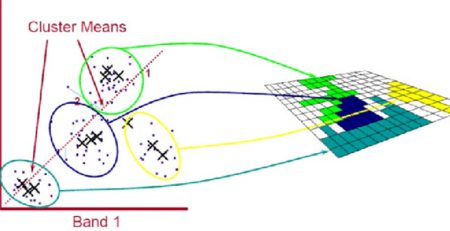


دیدگاه (2)
ممنون از مقاله خوبتون
سپاسگزاریم.