الگوریتم K-Means

مقدمه ای بر الگوریتم K-Means :

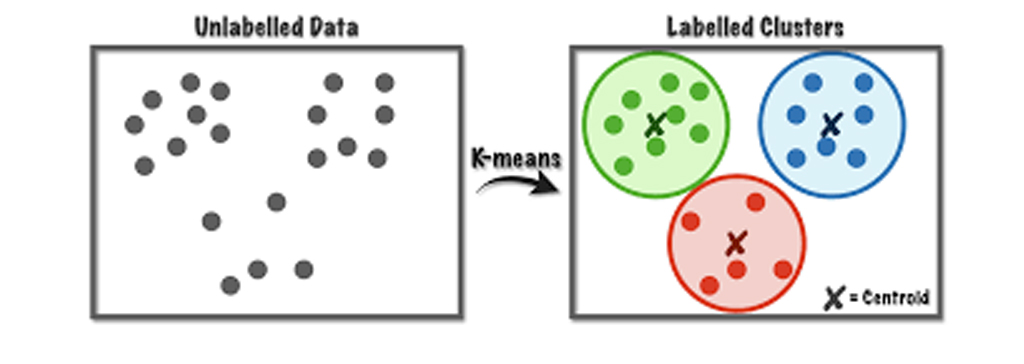
الگوریتم K-Means یک الگوریتم یادگیری بدون نظارت است که برای حل مشکلات خوشه بندی در یادگیری ماشین یا علم داده استفاده می­شود. در این مبحث به بررسی الگوریتم خوشه بندی K-Means می­پردازیم. خوشه‌بندی K-Means روشی در کمی‌سازی بردارهاست که در اصل از پردازش سیگنال گرفته شده و برای آنالیز خوشه بندی در داده کاوی محبوب است. هدف الگوریتم K-Means خوشه­ بندی k مشاهده به n  خوشه است که در آن هر یک از مشاهدات متعلق به خوش­ه ای با نزدیکترین میانگین به آن است، این میانگین به عنوان ‌نمونه استفاده می‌شود.

الگوریتم یادگیری بدون نظارت

الگوریتم یادگیری بدون نظارت : در یادگیری بدون نظارت یا یادگیری نظارت نشده مسئله به این صورت است که در این حالت داده‌هایی که داریم که پاسخ صحیح آن‌ها مشخص نیست و این داده‌ها برچسبی یکسان دارند و یا اصلاً برچسبی ندارند. پس مجموعه‌‌ای از داده در اختیار الگوریتم قرار می­گیرد که ساختار مشخصی ندارند؛ سپس الگوریتم یادگیری بدون نظارت (انواع مختلفی دارد مانند الگوریتم k-means، الگوریتم خوشه­ بندی سلسه مراتبی و… ) تشخیص می‌دهدکه چه داده ­هایی باید در یک خوشه قرار بگیرد.

الگوریتم خوشه ­بندی

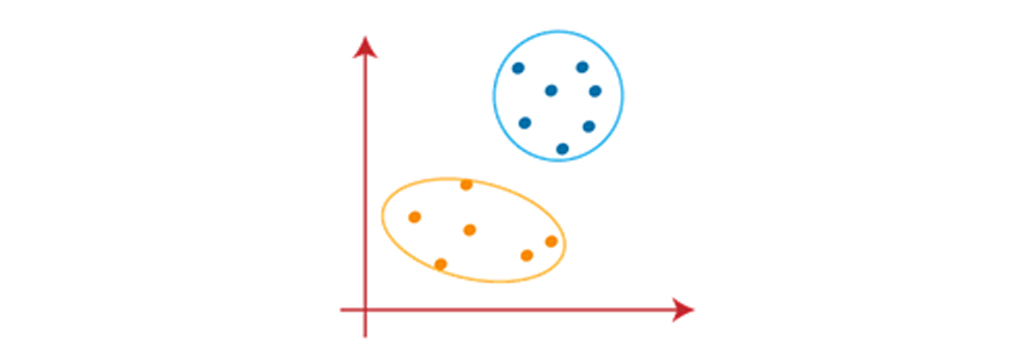
الگوریتم خوشه ­بندی یکی از متداول ­ترین روش تجزیه و تحلیل داده­ های اکتشافی است که برای دریافت شهودی در مورد ساختار داده ­ها استفاده می­شود. این روش می­تواند به عنوان وظیفه ­ی شناسایی زیرگروه ­ها در داده­ ها تعریف شود به این صورت که نقاط داده در یک زیر گروه (خوشه) بسیار شبیه به هم هستند در حالی که نقاط داده در خوشه­ های مختلف بسیار متفاوت هستند.

به عبارت دیگر، ما سعی می­کنیم زیرگروه­ های همگن را در داده ­ها پیدا کنیم، به این ترتیب که نقاط داده در هر خوشه با توجه به اندازه گیری شباهت مانند فاصله مبتنی بر اقلیدس یا فاصله مبتنی بر همبستگی، تا حد امکان شبیه هستند. تصمیمی که برای اندازه ­گیری شباهت از چه نوع فاصله­ ای استفاده شود خاص  هر داده  و برنامه است.

در این مطلب خوشه­ بندی را براساس ویژگی­ ها بررسی خواهیم کرد. به طور مثال خوشه ­بندی در تقسیم بازار استفاده می­شود؛ جایی که ما سعی می­کنیم مشتریانی پیدا کنیم که از نظر رفتار یا ویژگی مشابه یکدیگر باشند؛ جایی که ما سعی می­کنیم مناطق مشابه را با هم گروه ­بندی کنیم، خوشه­ بندی اسناد را بر اساس موضوعات و دیگر ویژگی ­ها انجام دهیم.

برخلاف یادگیری تحت نظارت، خوشه بندی یک روش یادگیری بدون نظارت در نظر گرفته می­شود، زیرا  حقیقت خوبی برای مقایسه خروجی الگوریتم خوشه­ بندی با برچسب­های واقعی برای ارزیابی عملکرد آن وجود ندارد و فقط سعی می­شود ساختار داده ­ها را با گروه ­بندی نقاط داده در زیرگروه­ های مجزا بررسی کنیم.

الگوریتم K-Means

الگوریتم K-Means یک الگوریتم بر پایه ­ی تکراری است که سعی می­کند مجموعه داده­ ها را به زیرگروه­های متمایز بدون همپوشانی تعریف کند که به این زیر گروه­ ها خوشه گفته ­می­شود؛ که در این گروه ­ها هر نقطه داده فقط به یک گروه تعلق دارد. در این الگوریتم سعی می­شود نقاط داده درون خوشه ­ای را تا حد ممکن شبیه به هم ساخت و در عین حال خوشه­ ها را تا حد امکان متفاوت (دور) از هم تعریف کرد.

این الگوریتم داده ­ها را به یک خوشه اختصاص می­دهد به طوری که مجموع فاصله مربع شده بین نقاط داده و مرکز گروه (میانگین محاسبه تمام نقاط داده ­ای که به آن خوشه تعلق دارند) در حداقل باشد. هرچه تنوع کمتری در خوشه­ ها داشته باشیم، نقاط داده در یک خوشه همگن (مشابه) هستند. رویکردی که K-Means که برای حل مسئله دنبال می­کند Expectation-Maximization نامیده می­شود.

در اینجا K تعداد خوشه­ های از پیش تعریف شده­ ای را که باید در این فرآیند ایجاد شوند تعریف می­کند، کما اینکه K = 2 ، دو خوشه وجود دارد و برای K = 3 ، سه خوشه و غیره وجود دارد. K-Means یک الگوریتم تکراری است که مجموعه داده بدون برچسب را به k خوشه­ ی مختلف تقسیم می­کند به گونه ­ای که هر مجموعه داده فقط متعلق به یک گروه است که دارای ویژگی­های مشابه است.

به ما امکان می­دهد تا داده ­ها را در گروه ­های مختلف قرار دهیم و راهی مناسب برای کشف دسته­ های گروه­ها در مجموعه داده ­های بدون برچسب و بدون نیاز به هیچ گونه آموزش وجود دارد. این یک الگوریتم مبتنی بر مرکز است که در آن هر خوشه با یک مرکز ارتباط دارد. هدف اصلی این الگوریتم به حداقل رساندن مجموع فواصل بین نقطه داده و خوشه های مربوطه است.

الگوریتم K-Means ، مجموعه داده بدون برچسب را به عنوان ورودی می­گیرد، مجموعه داده را به تعداد k خوشه تقسیم می­کند و روند را تکرار می­کند تا زمانی که بهترین خوشه ­ها را پیدا نکند الگوریتم ادامه پیدا می­کند. مقدار k باید در این الگوریتم از پیش تعیین شده باشد. عملکرد الگوریتم خوشه بندی k-mean به صورت زیر است:

با استفاده از یک فرایند تکرار، بهترین مقدار را برای نقاط مرکز تعیین می­کند. هر نقطه داده را به نزدیکترین مرکز k خود اختصاص می­دهد. آن نقاط داده ­ای که نزدیک مرکز k هستند، خوشه­ ای را ایجاد می­کنند. از این رو هر خوشه دارای نقاط داده با برخی نقاط مشترک است و از خوشه­ های دیگر دور است. نمودار زیر نحوه کارکرد الگوریتم خوشه بندی K-means را توضیح می دهد:

نحوه کار الگوریتم K-Means

نحوه کار الگوریتم K-Means در مراحل زیر توضیح داده شده است:

مرحله 1: برای تصمیم گیری در مورد تعداد خوشه ­ها ، تعداد K را انتخاب می­شود.

مرحله 2:  K تا از نقاط را به صورت تصادفی یا با محاسبه  انتخاب می­شود. (این می­تواند غیر از مجموعه داده ورودی باشد). بر اساس کد زیر از فاصله­ی اقلیدوسی برای انتخاب مراکز استفاده شده است.

مرحله 3: هر نقطه داده را به نزدیکترین مرکز خود اختصاص می­دهد، که خوشه­ های K از پیش تعریف شده را تشکیل می­دهد.

مرحله 4: میانگین را محاسبه کرده و یک مرکز جدید برای هر خوشه قرار می­دهد.

مرحله 5: مراحل سوم را تکرار می­شود، به این معنی که هر پایگاه داده را به جدیدترین و نزدیکترین مرکز هر خوشه اختصاص می­دهد.

 مرحله 6: اگر تغییر مجددی اتفاق افتاد، سپس  مرحله 4 مجدد اجرا می­شود و الگوریتم به پایان می­رسد.

مرحله 7: مدل آماده است.

مثال الگوریتم K-Means

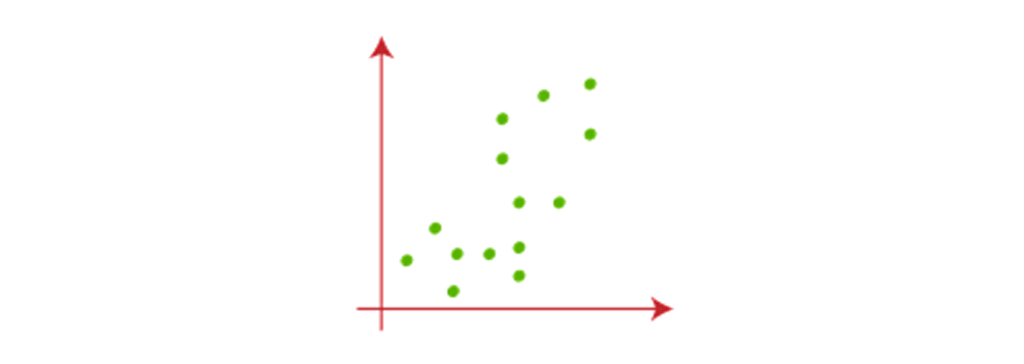
مثال الگوریتم K-Means : مراحل بالا را با در نظر گرفتن طرح های بصری می­توان درک بهتری ایجاد کرد: فرض کنید دو متغیر M1 و M2 داریم. نمودار پراکندگی محور x-y، این دو متغیر در زیر آورده شده است:

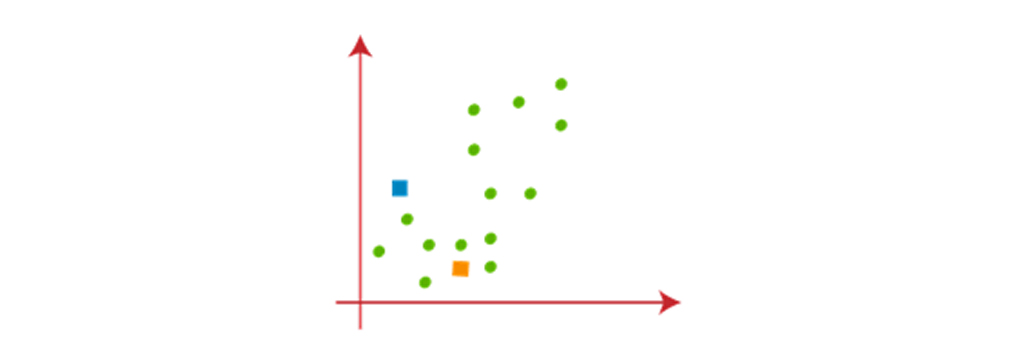
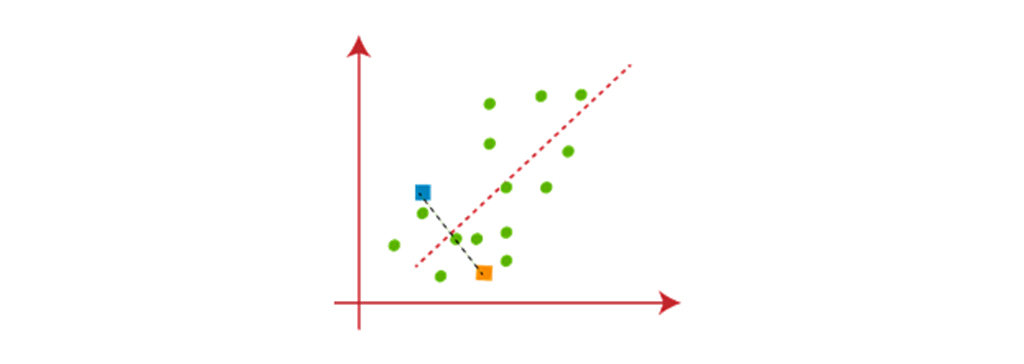
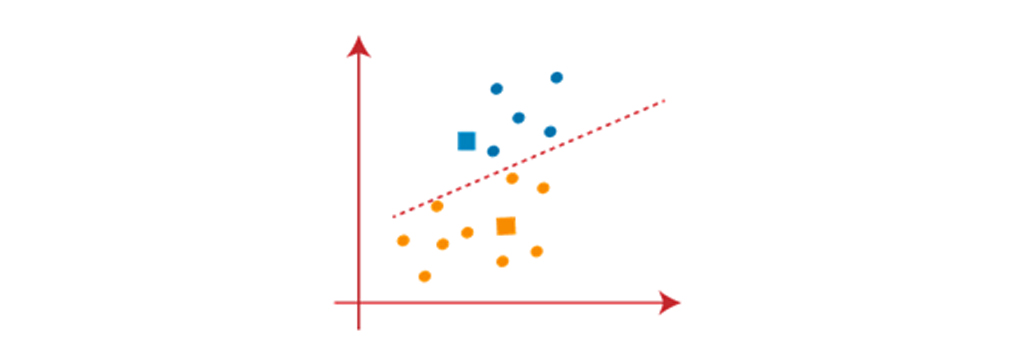
برای شناسایی مجموعه داده و قرار دادن آنها در خوشه ­های مختلف، تعداد k خوشه، یعنی K = 2 رادر نظر می­گیریم. به این معنی که در اینجا سعی می­کنیم این مجموعه داده­ ها را در دو خوشه مختلف گروه بندی کنیم. برای تشکیل خوشه باید K تا از نقاط را تصادفی به عنوان مرکز انتخاب کنیم. این نقاط می­توانند یا نقاط موجود در مجموعه داده یا هر نقطه دیگری باشند. بنابراین، در اینجا ما دو نقطه زیر را به عنوان k نقاط انتخاب می­کنیم، که بخشی از مجموعه داده ما نیستند دو نقطه ای که به صورت مربع و با رنگ نارنجی و آبی نشان داده شده ­اند. تصویر زیر را در نظر بگیرید:

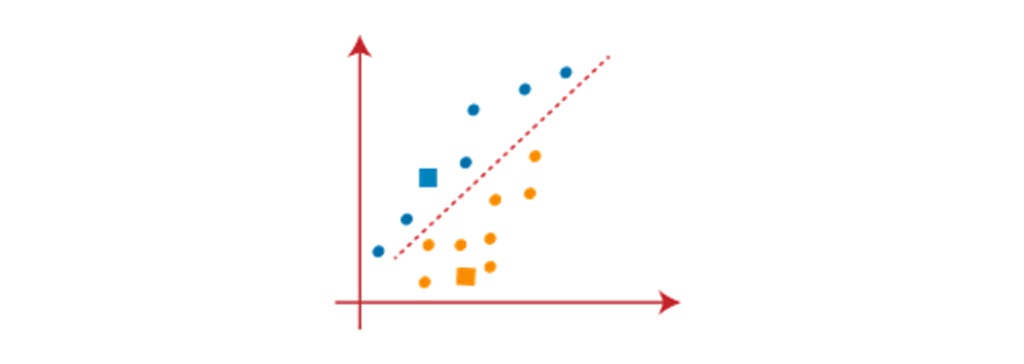
حال هر نقطه داده از نمودار پراکندگی را به نزدیکترین نقطه K یا مرکز آن اختصاص می­دهیم. با استفاده فرمول­ های ذکر شده در بالا، محاسبات را انجام می­شود. بنابراین، یک میانه بین هر دو مرکز ترسیم خواهد شد. تصویر زیر را در نظر بگیرید:

اکنون هر نقطه ای از نمودار پراکندگی به نزدیکترین نقطه K یا مرکز آن اختصاص پیدا می­کند. محاسبه فاصله بین دو نقطه با استفاده از فرمول ذکر شده در الگوریتم انجام می­شود. یک میانه بین هر دو مرکز ترسیم شده است. تصویر زیر را در نظر بگیرید:

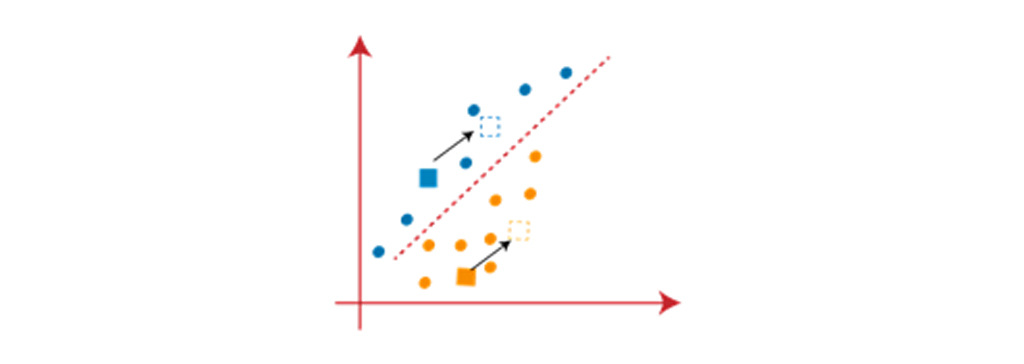
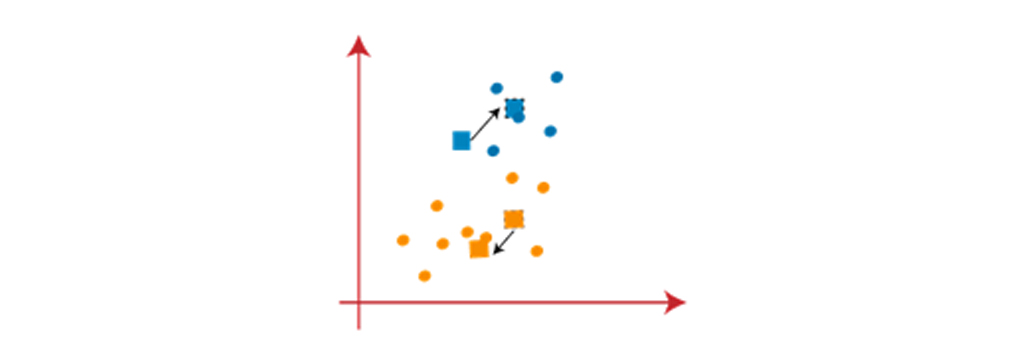
همانطور که باید نزدیکترین خوشه را پیدا کنیم، بنابراین با انتخاب مرکز فرآیند را تکرار خواهیم کرد. برای انتخاب مرکز جدید، مرکز ثقل این خوشه  محاسبه خواهد شد، و مرکز جدید را به صورت زیر  انتخاب می­شود:

در مرحله ­بعد، هر داده به مرکز جدید اختصاص پیدا می­کند. بدین منظور الگوریتم همان روند پیدا کردن یک خط میانه را تکرار می­کند. میانه مانند تصویر زیر خواهد بود:

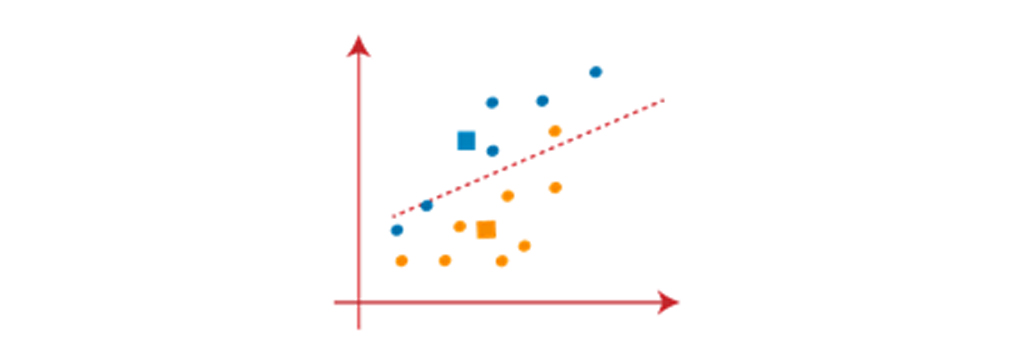
در تصویر بالا، می­بینیم که یک نقطه نارنجی در سمت چپ خط قرار دارد و دو نقطه آبی به سمت راست خط است. بنابراین، این سه نقطه به مراکز جدید اختصاص داده می­شود.

همانطور که گفته شد تغییر انجام شده است، بنابراین به طور مجدد مرحله ­ی 4 اجرا می­شود که یافتن مراکز یا نقاط K جدید است. ما با یافتن مراکز این فرایند را تکرار خواهیم کرد، بنابراین مراکز جدید مانند تصویر زیر نشان داده می­شوند:

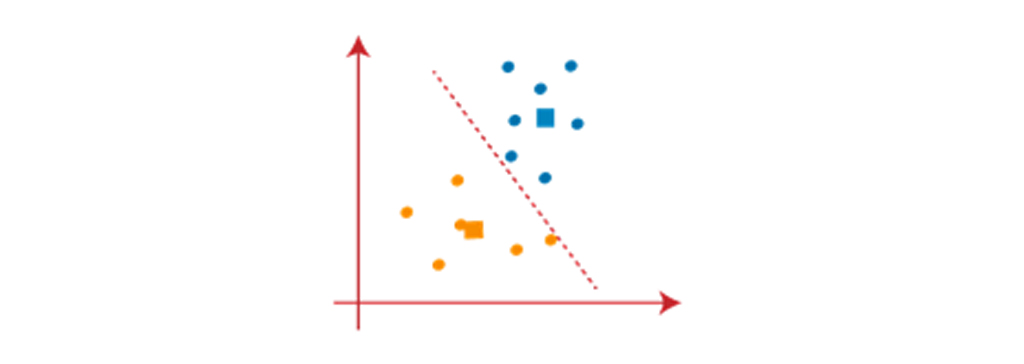
همانطور که مراکز جدید را بدست می­اید، بنابراین دوباره خط میانی ترسیم کرده و نقاط داده را مجدداً تعیین می­کنیم. بنابراین، تصویر زیر را در ادامه خواهیم داشت:

در تصویر بالا می­بینیم که هیچ نقطه داده غیر متفاوتی در دو طرف خط وجود ندارد، این بدان معنی است که مدل ما شکل گرفته است. تصویر زیر را در نظر بگیرید:

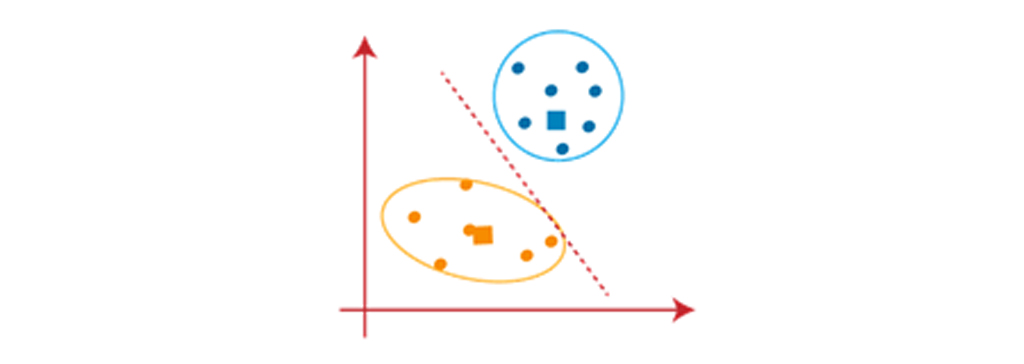
همانطور که مدل ما آماده است، بنابراین اکنون می­توانیم مراکز فرض شده را حذف کنیم و دو خوشه نهایی همانطور که در تصویر زیر نشان داده شده است را به عنوان دو خوشه­ ی نهایی فرض کنیم.

مراحل بالا دسته بندی یک سری داده به صورت کاملا فرضی و برای درک بهتر الگوریتم K-means بوده است.

در الگوریتم k-means بعد از انجام چندین مرحله اگر تغییری در خوشه‌ی هر کدام از نمونه‌ها رخ نداد یعنی با توجه به شکل بالا نقاط آبی، آبی ماندند و نقاط نارنجی نیز نارنجی مانند الگوریتم به پایان می­رسد و این یکی از شروطی است که می‌تواند الگوریتم را خاتمه دهد. یعنی الگوریتم وقتی به این حالت رسید که در چند دورِ متوالی تغییری در خوشه‌ی نمونه‌ها به وجود نیامد، به این معنی است که  این حالتِ پایانی برای خوشه‌ها اتفاق افتاده است.

حالت دوم برای خاتمه ­ی الگوریتم تعریف تعداد دورهای اجرای الگوریتم است به طور مثال می­توان گفت این الگوریتم 20 بار اجرا شود و بعد از 20 بار اجرای الگوریتم نتیجه را مشاهد کرد که اغلب این روش برای یافتن بهترین دور اجرا استفاده می­شود. به طور کل در الگوریتم‌های مبتنی بر تکرار (iterative algorithms) می‌توان تعدادِ تکرارها را محدود کرد تا الگوریتم بی‌نهایت تکرار نداشته باشد.

اندازه گیری فاصله در k-means

اندازه گیری فاصله، تشابه بین دو عنصر را تعیین می­کند و بر شکل خوشه­ها تأثیر می­گذارد. خوشه بندی در K-Means از انواع مختلف اندازه گیری فاصله مانند موارد زیر پشتیبانی می­کند: ( اندازه گیری فاصله در k-means )

• اندازه گیری فاصله اقلیدسی (فاصله­ ی اقلیدسی یکی از پرکاربردترین و محبوب ترین فاصله ­ها در الگوریتم ­های مبتنی بر فاصله است.)
• اندازه گیری فاصله منهتن
• اندازه گیری فاصله اقلیدسی در مربع
• اندازه گیری فاصله کسینوس

کاربرد الگوریتم K-Means

از کاربرد الگوریتم K-Means می توان به موارد زیر اشاره کرد:

• سنجش عملکرد تحصیلی ( بر اساس نمرات، دانش آموزان در نمرات A ، B یا C طبقه بندی می­شوند).
• سیستم­های تشخیصی ( سیستم ­های تشخیصی حرفه ­ای پزشکی در ایجاد سیستم ­های پشتیبانی دقیق تصمیم پزشکی، به ویژه در درمان بیماری ­های کبدی، شناسایی بیماری قلبی و شناسایی تومرها و بررسی تاثیر داروها)
• موتورهای جستجو
• شبکه های حسگر بی سیم
• تقسیم بازار ( تقسیم­ بندی بازار، تقسیم­ بندی مشتریان به منظور تعیین مشتری هدف و تبلیغات هدفمند وتاثیرگذار)
• تقسیم تصویر و فشرده سازی تصویر و پردازش تصویر

مزایا الگوریتم K-Means

روش خوشه بندی k-means ساده ­ترین روش برای خوشه ­بندی داده ­ها است. از مزایا الگوریتم K-Means می‌توان به موارد زیر اشاره کرد:

• سرعت بسیار بالای این روش در اجرا.
• استفاده از این الگوریتم بسیار ساده ( با استفاده از کتابخانه ­ها و پکیج­ های اماده مربوط به این الگوریتم) است.
• این الگوریتم برای داده­ هایی با حجم زیاد قابل استفاده است.
• این الگوریتم همگرایی را تضمین می­کند.
• این الگوریتم بهترین موقعیت­ ها برای مراکز را در نظر می­گیرد.
• این روش به راحتی با نمونه­ های جدید سازگار می­شود.
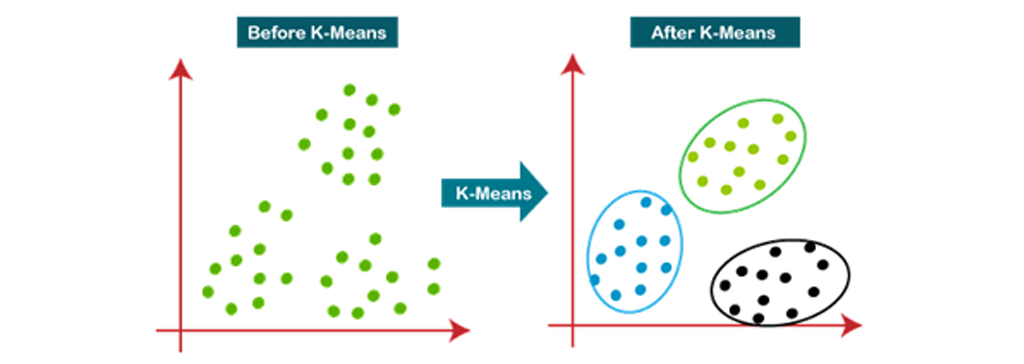
• خوشه ­هایی با شکل و اندازه­ های مختلف مانند خوشه ­های بیضوی تعمیم می­یابد.

معایب الگوریتم K-Means

از معایب الگوریتم K-Means می‌توان به موارد زیر اشاره کرد:

• نیاز داشتن به تعیین تعدادخوشه ­ها.
• این الگوریتم دارای دقت کم در داده ­ها با شکل غیر محدب است.

جمع بندی الگوریتم K-Means

الگوریتم K-Means بسیار محبوب است و در برنامه ­های مختلفی مانند تقسیم بازار، خوشه­ بندی اسناد، تقسیم تصویر و فشرده سازی تصویر و غیره مورد استفاده قرار می­گیرد. این الگوریتم یک الگوریتم تکرار شونده است که مجموعه داده را با توجه به ویژگی های آنها به تعداد K خوشه­ های متمایز غیر همپوشانی از پیش تعریف شده تقسیم می­کند.

این باعث می­شود نقاط داده بین خوشه­ ها تا حد ممکن مشابه باشند و همچنین سعی دارد خوشه ها را تا حد ممکن حفظ کند. اگر مجموع فاصله مربع بین مرکز خوشه و نقاط داده در حداقل باشد، داده ها را به یک خوشه اختصاص می­دهد. تنوع کمتری در خوشه باعث ایجاد داده­ های مشابه یا همگن در خوشه می شود.

هدف معمولاً هنگامی که تجزیه و تحلیل خوشه انجام می­دهیم این است که از ساختار داده ­هایی که با آنها سر و کار داریم، یک شهود معنادار دریافت کنیم. اگر اعتقاد داشته باشیم که تنوع زیادی در رفتارهای زیرگروه­های مختلف وجود دارد، خوشه­ بندی برای پیش­بینی رفتار پدیده ­های مختلف بسیار موثر است.

نویسنده: تیم پژوهش راهبرد

 

منابع

towardsdatascience.com

javatpoint.com