الگوریتم k-medians
الگوریتم k-medians یا الگوریتم k میانه ها
در حوزه کامپیوتر به دلیل تنوع باور نکردنی الگوریتم های کاربردی آن، با الگوریتم های مختلف مواجه می شویم این الگوریتم ها به دو دسته یادگیری بدون نظارت یا یادگیری با نظارت، تقسیم می شوند که این ها شامل طبقه بندی، داده کاوی و … است. k-medians و الگوریتم k-means دو رویکرد رایج برای انجام کار خوشه بندی در داده کاوی هستند. وظیفه خوشه بندی هر یک از این الگوریتم ها شامل یافتن مراکز خوشه ای بدین منظور که مجموع فاصله بین یک مرکز و همه نقاط موجود در آن خوشه به حداقل برسد. تفاوت دو روش در نحوه ی یافتن “مرکز” خوشه است. همانطور که می توان با نام آن ها استنباط کرد، k-means از میانگین برای حداقل رساندن فاصله ها استفاده می کند، در حالی که k-medians از میانه برای یافتن مراکز هر خوشه استفاده می کند. در این مطلب به بررسی الگوریتم k-medians می پردازیم. پس با راهبرد همراه باشید.
خوشه بندی
خوشه بندیخوشهبندی جز روش های است که برای تحلیل کردن داده ها و اطلاعات به کار می رود. در این روش نقاط داده را به جهت «ماکسیمم کردن شباهت های درون خوشه و مینیمم کردن شباهت با نقاط داده خارج خوشه»، بدون استفاده از برچسب های(Label) از قبل تعیین نشده برای نقاط داده (یادگیری نظارت نشده)، خوشه بندی انجام می دهد.
الگوریتم k-medians
الگوریتم k-medians که به آن Partitioning Around Medoid نیز گفته می شود در سال 1987 توسط کافمن و روسیو پیشنهاد شد. در این الگوریتم مراکز را می توان نقطه ای در خوشه تعریف کرد که فاصله های آن با سایر نقاط خوشه حداقل است. همانطور که در بالا گفته شد، k-medians در خوشه بندی کردن داده ها تلاش می کند تا بتواند فاصله های 1-norm بین هر نقطه و نزدیکترین مرکز خوشه ای آن را به حداقل برساند. این با تنظیم مرکز، حداقل فاصله ها به دست می آید که مرکز هر خوشه میانه تمام نقاط آن خوشه باشد. در این بخش به بحث در مورد اینکه چرا این روش بسیار قدرتمند است می پردازیم.
چرا از k-medians برای یافتن مراکز خوشه ای استفاده می شود؟
مشکل k-means خیلی قبل از k-medians پیش بینی شده بود. K-medians قدرت خود را مدیون استحکام میانه به عنوان یک پارامتر آماری است. میانگین یک اندازه گیری است که بسیار در معرض تغییرات زیاد است. حتی فقط یک داده نویز یا خارج از محدوده می تواند مقدار میانگین را بسیار تغییر دهد و این موجب ایجاد اشتباه می شود. یکی از موارد نگرانی در امر خوشه بندی زمانی است که از k-means بر روی مجموعه داده های بسیار بزرگ استفاده می شود که امکان دارد داده های خارج از محدوده زیاد باشد و بر روی خوشه بندی تاثیر نادرست بگذارد. دلیل برتری k-mediansدر خوشه بندی نسبت به k-means این است که میانه یک آمار فوق العاده مقاوم نسبت به داده های بسیار دور است. این فاکتور آماری برای خطا، حداقل به 50 درصد داده ها نیاز دارد تا میانه اشتباه را تعیین کند. بنابراین این الگوریتم می تواند بسیار مقاوم تر در مجموعه داده های بزرگ عمل کند.
الگوریتم k-medians بر اساس جستجوی k اجسام نماینده یا میانه در بین مشاهدات مجموعه داده ها است. پس از یافتن مجموعه ای از k-medians، خوشه ها با اختصاص هر مشاهده به نزدیکترین میانه ساخته می شوند. در مرحله بعد، هر m میانه انتخاب شده و هر نقطه داده غیر از میانه ها جابجا شده و تابع هدف برای این داده ها محاسبه می شود. تابع هدف با مجموع شباهت های همه اجسام با نزدیکترین میانه آن ها مطابقت دارد. مرحله جا به جایی تلاش می کند تا کیفیت خوشه را با تبادل داده های انتخاب شده (میانه ها) و داده های انتخاب نشده بهبود بخشد. اگر بتوان تابع هدف را با تعویض یک داده انتخاب شده با یک داده انتخاب نشده کاهش داد، مبادله انجام می شود. این کار تا زمانی ادامه می یابد که دیگر نمی توان تابع هدف را کاهش داد. هدف این است که k میانه را به عنوان نماینده، پیدا کنیم که مجموع فاصله داده ها را با نزدیکترین داده نماینده آن ها به حداقل برسانیم.
مراحل موجود در الگوریتم k-medians یا الگوریتم k میانه ها
مرحله ساخت(Build phase):
1- k داده را برای تبدیل شدن به مراکز انتخاب کنید، یا در صورت ارائه این داده از آن ها به عنوان میانه یا مرکز استفاده کنید.
2- ماتریس عدم تشابه را در صورت عدم ارائه محاسبه کنید.
3- هر شی را به نزدیکترین مرکز خود اختصاص دهید.
مرحله تعویض(Swap phase):
4- برای هر جستجوی خوشه ای، اگر هر یک از اجزای خوشه میانگین ضریب عدم شباهت را کاهش دهد. در این صورت، داده ای که در این ضریب بیشترین کاهش را ایجاد می کند، به عنوان مرکز این خوشه انتخاب کنید.
5- اگر حداقل یک مرکز تغییر کرده است به مرحله (3) بر می گردیم، در غیر این صورت الگوریتم را خاتمه می یابد.
نکته.همانطور که در بالا ذکر شد، الگوریتم k-medians با ماتریسی از فاصله کار می کند و برای محاسبه این ماتریس، الگوریتم می تواند از دو معیار استفاده کند:
فواصل اقلیدسی، که مجموع مربع اصلی تفاوت ها هستند.
فاصله منهتن که مجموع فاصله های مطلق است. استفاده از معیار فاصله منهتن در این الگوریتم بسیار رایج تر است. فاصله بین مرکز c i و داده p i از فرمول زیر محاسبه می شود:
برای محاسبه تابع هزینه در الگوریتم k-medians با فرمول زیر محاسبه می شود.
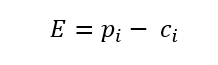
مثال الگوریتم k-medians یا الگوریتم k میانه ها
به مثالی از الگوریتم k-medians توجه کنید:
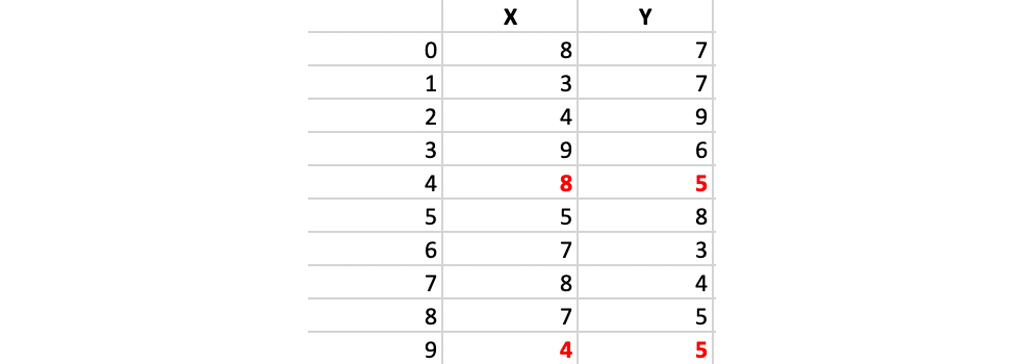
اگر نمودار با استفاده از نقاط داده بالا ترسیم شود، موارد زیر را بدست می آوریم:
مرحله 1: اجازه دهید 2 مرکز به طور تصادفی انتخاب شوند. بنابراین k = 2 را انتخاب کنید.
اجازه دهید (4.5) = c1 و (8.5) = c2 دو مرکز انتخابی باشند.
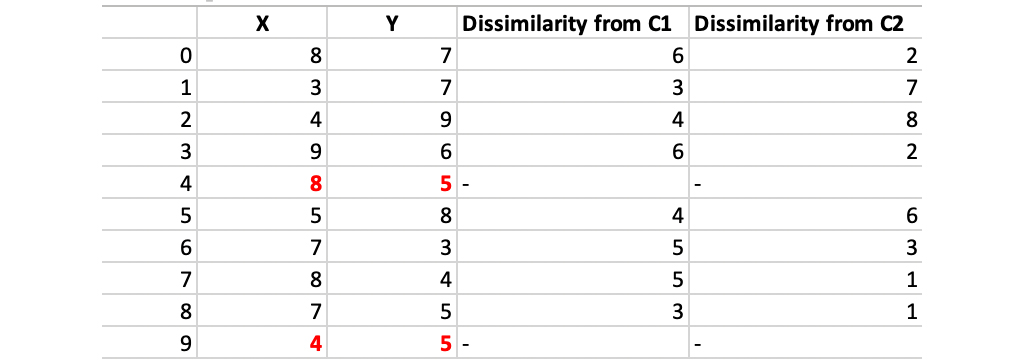
مرحله 2: محاسبه هزینه عدم شباهت هر نقطه غیر مرکز با مرکز محاسبه و جدول بندی می شود:
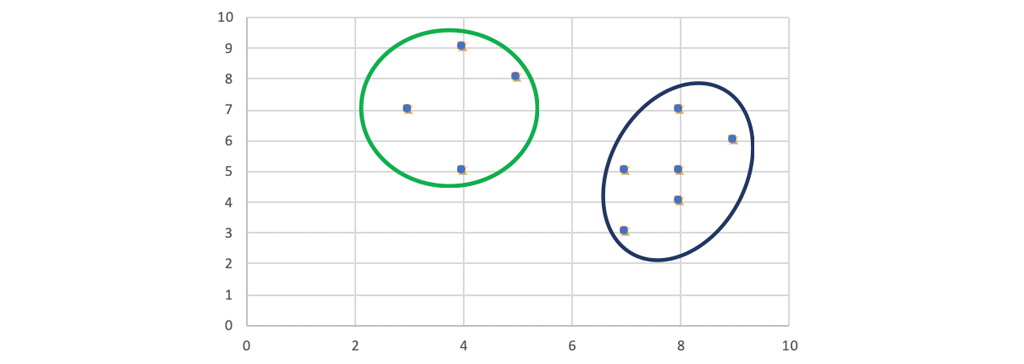
هر نقطه به خوشه آن مرکزی اختصاص داده می شود که فاصله آن کمتر است. نقاط 1 ، 2 ، 5 به خوشه c1 و 0 ، 3 ، 6 ، 7 ، 8 به خوشه c2 می رسد.
هزینه = (3 + 4 + 4) + (3 + 1 + 1 + 2 + 2) = 20
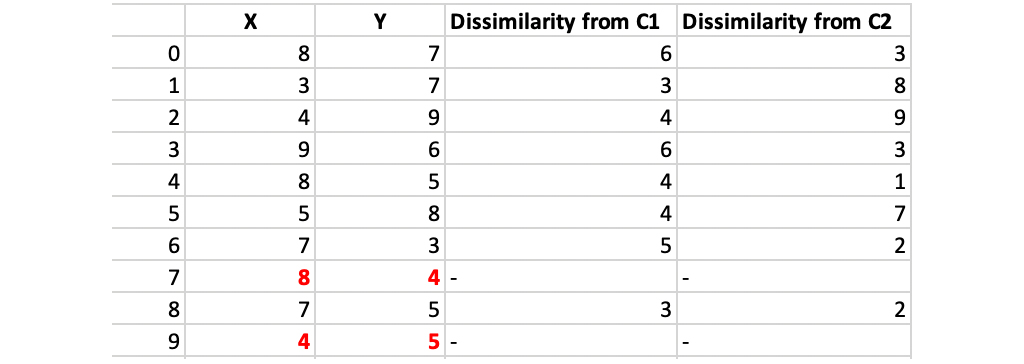
مرحله 3: به طور تصادفی یک نقطه غیر از مراکز انتخابی را انتخاب کرده و هزینه را دوباره محاسبه کنید. اجازه دهید نقطه تصادفی انتخاب شده (8.4) باشد.
عدم شباهت هر نقطه غیر مرکز با مراکز (4.5) = c1 و (8.4) = c2 و محاسبه و جدول بندی می شود.
هر نقطه به آن خوشه اختصاص داده می شود که که فاصله ی آن با مرکزش کمتر است. بنابراین ، نقاط 1 ، 2 ، 5 به خوشه c1 و 0 ، 3 ، 6 ، 7 ، 8 به خوشه c2 می رسد.
مقدار تابع هزینه جدید = (3 + 4 + 4) + (2 + 2 + 1 + 3 + 3) = 22
هزینه مبادله = هزینه جدید – هزینه قبلی = 22 – 20
و 2> 0 از آنجا که هزینه مبادله کمتر از صفر نیست، ما جا به جایی را لغو می کنیم. از این رو
(4.5) = c1 و (8.4) = c2 مرکز های نهایی هستند. خوشه بندی به شکل زیر خواهد بود.
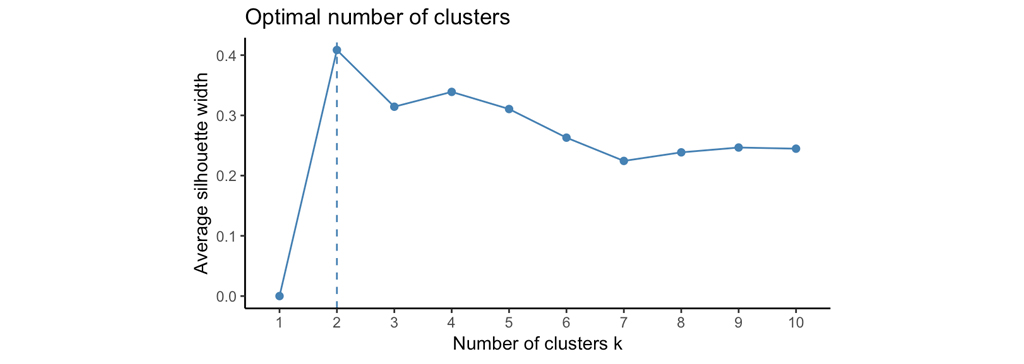
محاسبه تعداد بهینه خوشه ها
برای برآورد تعداد مطلوب خوشه ها، یکی از روش های پیشنهادی روش silhouette average است. این روش به این صورت است که الگوریتم k-medians را با استفاده از مقادیر مختلف تعدادخوشه ها k را محاسبه می کند. در مرحله بعد، اندازه متوسط خوشه ها با توجه به تعداد خوشه ها ترسیم می شود. silhouette average کیفیت خوشه بندی را اندازه گیری می کند. عرض silhouette average بالا نشان دهنده خوشه بندی خوب است. تعداد بهینه خوشه ها k است که silhouette average را در محدوده مقادیر ممکن برای k حداکثر می کند.
بنابر این نمودار، تعداد خوشه های پیشنهادی 2 است. با تقسیم داده های موجود به دو خوشه بهترین تقسیم بندی را برای داده های بالا خواهیم داشت و بهترین نتیجه گیری و تفسیر را می توان انجام داد.
مزایای الگوریتم k-medians:
1- درک الگوریتم k-medians ساده است و پیاده سازی آن بسیار آسان است.
2- الگوریتم k-medians سریع است و در تعداد گام های ثابت همگرا می شود.
3- الگوریتم k-medians نسبت به سایر الگوریتم های خوشه بندی نسبت به داده های خارج از رنج کم تر حساس است.
معایب الگوریتم k-medians:
1- معایب اصلی الگوریتم های k-medians این است که برای خوشه بندی گروه های غیر کروی (شکل دلخواه) از داده مناسب نیست. این به این دلیل است که به حداقل رساندن فاصله بین داده های غیر مرکز و مرکز به مرکز خوشه متکی است. این الگوریتم به طور خلاصه، از فشردگی به عنوان معیار خوشه بندی به جای تلفیق استفاده می کند.
2- ممکن است نتایج متفاوتی را برای اجراهای مختلف در یک مجموعه داده یکسان بدست آورد زیرا اولین k مرکز به طور تصادفی انتخاب می شوند.
کاربردهای الگوریتم خوشه بندی k-medians
خوشه بندی کاربرد های بسیار دارد از کاربرد خوشه بندی در این جا به مهم ترین کاربرد های آن اشاره کرد:
بازاریابی: یکی از مهم ترین کاربرد های خوشه بندی در بحث بازاریابی است. از انواع الگوریتم های خوشه بندی می توان در حوزه های مختلف بازاریابی و شناسایی فرصت های موجود در بازار استفاده کرد. از این الگوریتم ها برای بررسی و کشف رفتار مشتری، دسته بندی مشتری، تحلیل سبد خرید مشتری و تبلیغات هدفمند استفاده کرد.
زیست شناسی: از دیگر کاربرد های خوشه بندی در تقسیم بندی گونه های گیاهی و جانوری مختلف است. این روش به زیست شناسان برای کشف گونه های جدید و تفسیر نتایج بسیار کمک می کند.
بیمه و بانک: از روش های خوشه بندی برای تقسیم بندی مشتریان و خدمات ارائه شده به ان ها استفاده می شود. با استفاده از این روش ها می توان کلاهبرداری ها را به راحتی شناسایی کرد.
تحلیل شبکه اجتماعی: استفاده از اطلاعات استخراجی از یک شبکه ی اجتماعی بسیار پر کاربرد است. با استفاده از تحلیل این شبکه ها و گراف های حاصل از ارتباط این شبکه ها، امکان بر قراری ارتباطات جدید با پیشنهاهایی بر اساس این تحلیل ها امکان پذیر می شود. این ارتباطات گاهی برای یافتن یک دوست قدیمی استفاده می شود و گاهی از این اطلاعات برای تبلیغات هدفمند نیز استفاده می شود.
گروه بندی نتایج جستجو: موتور های جست و جو با اطلاعات بسیار زیادی مواجه هستند بنابراین از الگوریتم های پرکاربرد در موتورهای جست و جو الگوریتم های خوشه بندی است تا بتوانند بهترین نتیجه را برای کاربر نشان دهند.
تصویربرداری پزشکی و پزشکی: برای تحلیل تصاویر پزشکی و تشخیص بیماری می توان از روش های مختلف خوشه بندی استفاده کرد. این کار به پزشکان در تشخیص بیماری، میزان پیشرفت بیماری و بررسی تاثیر دارو بر روی بیماران استفاده می شود.
کتابخانه: در خوشه بندی کتاب های مختلف بر اساس موضوعات، نویسند سال چاپ و اطلاعات، کتاب ها خوشه بندی می شوند و دسترسی و یافتن اطلاعات بسیار آسان تر می شود
برنامه ریزی شهری: برای دسته بندی اطلاعات مربوط به مناطق مختلف شهری و موقعیت های مختلف جغرافیایی از روش های خوشه بندی استفاده می شود. و با استفاده از نتایج ان می توان برای قیمت گذاری املاک استفاده کرد.
سیستم توصیه گر: با استفاده از سیستم های توصیه گر می توان موارد مشابه را بررسی کرد و به کاربران ایتم های مشابه با سلیقه ی ان ها را پیشنهاد داد. این پیشنهاد ها می تواند بر اساس الگوهای استخراجی باشد که نتایج جست و جوی های قبلی کاربر است. از این روش برای پیشنهاد دادن کالاهای جدید یا فیلم و یا موزیک جدید است.
بخش بندی تصویر: از الگوریتم های خوشه بندی می‌توان برای بخش بندی تصاویر دیجیتال استفاده کرد. از این تقسیم بندی ها برای تحلیل این تصاویر استفاده می شود.
رباتیک: از خوشه بندی برای تقسیم بندی ربات ها از لحاظ کاربرد و موقعیت یابی آن ها استفاده می شود.
جمع بندی الگوریتم k-medians یا الگوریتم k میانه ها
الگوریتم k-medians یا الگوریتم k میانه ها، یک جایگزین قوی برای k-means است که برای تقسیم بندی مجموعه داده ها به خوشه های داده استفاده می شود. در روش k-medians، هر خوشه توسط یک شیء انتخاب شده در داخل خوشه نشان داده می شود. داده انتخاب شده مرکز نامیده می شود. الگوریتم k-medians از کاربر می خواهد که داده ها را وارد کند و تعداد خوشه های مناسب برای ایجاد شدن خوشه ها را به الگوریتم بدهد. این الگوریتم بسیار قوی است و برای خوشه بندی مجموعه داده های بزرگ استفاده می شود.
نویسنده: تیم پژوهش راهبرد
منابع
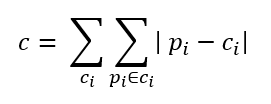
دیدگاهتان را بنویسید