رگرسیون خطی Linear Regression
سرفصل مطالب
مقدمه ای بر رگرسیون خطی Linear Regression :
اشخاص در رشته های مختلف سعی می کنند از هوش مصنوعی استفاده کنند تا کارهایشان بسیار آسان تر شود. به عنوان مثال، اقتصاددانان از هوش مصنوعی برای پیش بینی قیمت بازار در آینده برای کسب سود استفاده می کنند، پزشکان از هوش مصنوعی برای طبقه بندی بدخیم یا خوش خیم بودن تومور استفاده می کنند، هواشناسان برای پیش بینی آب و هوا از هوش مصنوعی استفاده می کنند، استخدام کنندگان منابع انسانی از هوش مصنوعی برای بررسی رزومه متقاضیان استفاده می کنند. محرک پشت چنین استفاده هایی AI و با استفاده از الگوریتم های یادگیری ماشین است. الگوریتم ابتدایی که همه علاقه مندان به یادگیری ماشین با آن شروع می کنند یک الگوریتم رگرسیون خطی است. در این مطلب به بررسی الگوریتم رگرسیون خطی می پردازیم.

رگرسیون خطی
رگرسیون روشی برای مدل سازی مقدار هدف بر اساس پیش بینی کننده های مستقل است. این روش بیشتر برای پیش بینی و یافتن رابطه علت و معلولی بین متغیرها استفاده می شود. تکنیک های رگرسیون بیشتر بر اساس تعداد متغیرهای مستقل و نوع رابطه بین متغیرهای مستقل و وابسته متفاوت است.
می توان آن را به عنوان روشی برای تجزیه و تحلیل آماری توصیف کرد که می تواند برای مطالعه رابطه بین دو متغیر کمی مورد استفاده قرار گیرد. در درجه اول، با استفاده از روش رگرسیون خطی ساده می توان به دو نکته پی برد: استحکام رابطه بین دو متغیر داده شده. (به عنوان مثال، رابطه بین گرم شدن کره زمین و ذوب شدن یخچال ها) و نکته بعدی مقدار متغیر وابسته در مقدار معینی از متغیر مستقل چقدر است. (به عنوان مثال ، میزان ذوب یخچال طبیعی در سطح مشخصی از گرمایش یا دمای کره زمین)
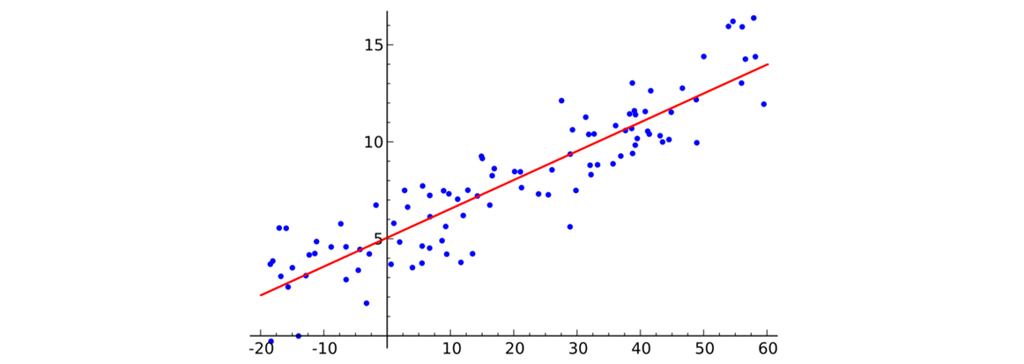
رگرسیون خطی ساده نوعی تحلیل رگرسیون است که در آن تعداد متغیرهای مستقل یک است و بین متغیر مستقل(x) وابسته (y) رابطه خطی وجود دارد. خط قرمز در نمودار بالا به عنوان مناسب ترین خط مستقیم معرفی شده است. بر اساس نقاط داده رسم شده، ما سعی می کنیم خطی را ترسیم کنیم که نقاط را به بهترین شکل مدل کند. می توان خط را بر اساس معادله خطی نشان داده شده در زیر مدل کرد.
انگیزه الگوریتم رگرسیون خطی یافتن بهترین مقادیر برای ß0 و ß1 است. قبل از بیان الگوریتم، بیایید نگاهی به دو مفهوم مهم داشته باشیم که برای درک بهتر رگرسیون خطی باید بدانیم.
تابع هزینه:
تابع هزینه به ما کمک می کند تا بهترین مقادیر ممکن برای و را که بهترین خط مناسب برای نقاط داده را فراهم می کند بیابیم. از آنجا که ما بهترین مقادیر را برای و می خواهیم ، این مشکل جستجو را به یک مشکل کوچک سازی تبدیل می کنیم که در آن می خواهیم خطا بین مقدار پیش بینی شده و مقدار واقعی را به حداقل برسانیم.
ما تابع بالا را برای به حداقل رساندن انتخاب می کنیم. تفاوت بین مقادیر پیش بینی شده و حقیقت موجود، تفاوت خطا را اندازه گیری می کند. اختلاف خطا را بر روی تمام نقاط داده جمع می کنیم و آن مقدار را بر تعداد کل نقاط داده تقسیم می کنیم. این میانگین خطای مربع را در تمام نقاط داده ارائه می دهد. بنابراین، این تابع هزینه به عنوان تابع خطای میانگین مربع(MSE) نیز شناخته می شود. اکنون، با استفاده از این تابع MSE، مقادیر و را طوری تغییر می دهیم که مقدار MSE در حداقل تنظیم شود.
نزول گرادیان
نزول گرادیان، مفهوم مهم بعدی مورد نیاز برای درک رگرسیون خطی است. نزول گرادیان روشی برای به روزرسانی مقادیر و برای کاهش عملکرد هزینه (MSE) است. ایده این است که با مقادیر و شروع می کنیم و سپس این مقادیر را به طور مکرر تغییر می دهیم تا هزینه کاهش یابد. نزول گرادیان به ما در نحوه تغییر ارزش ها کمک می کند.
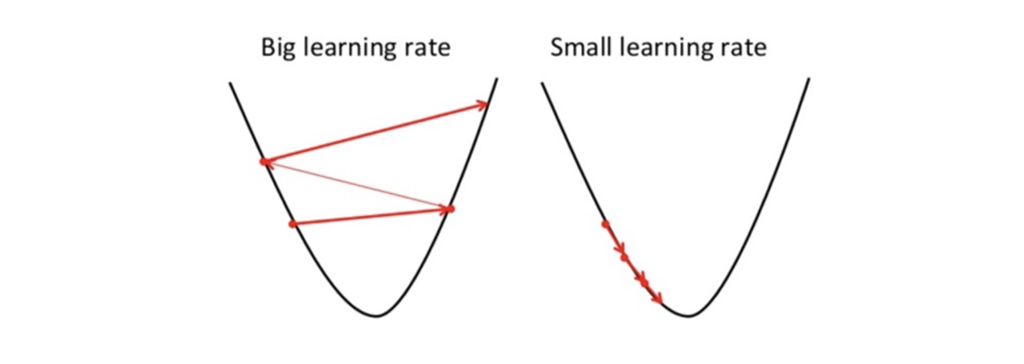
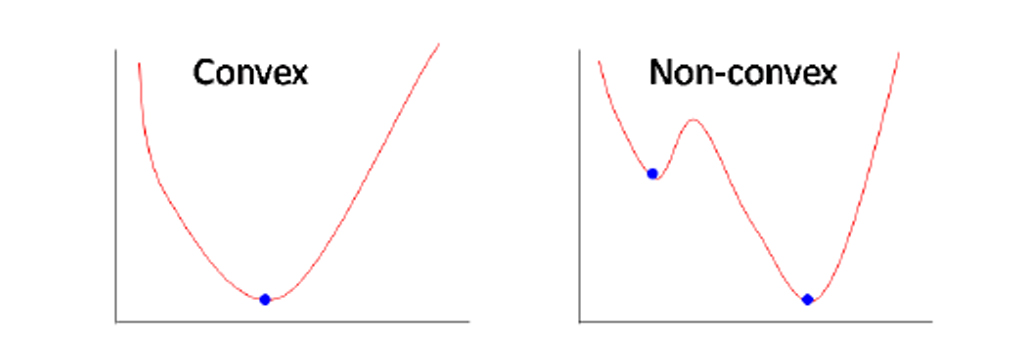
برای ترسیم این روش، گودالی را به شکل U تصور کنید و در بالاترین نقطه گودال ایستاده اید و هدف شما رسیدن به پایین گودال است. یک مشکل وجود دارد، فقط می توانید تعدادی گام گسسته برای رسیدن به پایین بردارید. اگر تصمیم بگیرید که گام به گام بروید، در نهایت به انتهای گودال می رسید، اما این مدت زمان بیشتری طول می کشد. اگر هر بار قدم های بلندتری بردارید، زودتر به آن می رسید، اما این احتمال وجود دارد که بتوانید از انتهای گودال فراتر بروید! نه دقیقاً در پایین. در الگوریتم نزول گرادیان، تعداد گام هایی که بر می دارید میزان یادگیری است. این گام تصمیم می گیرد که الگوریتم با چه سرعتی به حداقل برسد.
گاهی اوقات تابع هزینه می تواند یک تابع غیر محدب باشد که در آن می توانید در حداقل محلی قرار بگیرید اما برای رگرسیون خطی، همیشه یک تابع محدب است.
شاید برای شما این سوال پیش آمده باشد که چگونه می توان از شیب نزولی برای به روز رسانی و استفاده کرد. برای یافتن این شیب، مشتقات جزئی را با توجه به و در نظر می گیریم. در حال حاضر، برای درک نحوه یافتن مشتقات جزئی در زیر، نیاز به محاسبه داریم.
مشتقات جزئی شیب هستند و از آنها برای به روز رسانی مقادیر به و استفاده می شود. آلفا میزان یادگیری است که یک پارامتر فوق العاده است که باید آن را مشخص کنید. نرخ یادگیری کوچکتر می تواند شما را به حداقل ها نزدیک کند اما زمان بیشتری برای رسیدن به حداقل ها لازم است، میزان یادگیری بزرگتر زودتر همگرا می شود اما این احتمال وجود دارد که بتوانید از کمترین مقدار دور شوید.
خطا در رگرسیون خطی
در رگرسیون خطی قرار است خطی برای جدا کردن داده ها رسم کنیم هرچه این خط دقیق تر و منطبق تر بر داده ها باشد پیش بینی بهتر بوده و خطا کمتر است. همان طور که در شکل زیر می بینید خط آبی، خط رگرسیون است و نقاط قرمز، نقاط داده است و هم چنین خطوط سبز فاصله نقاط از خط آبی را نشان می دهد. این فاصله نقاط از خط آبی همان خطای رگرسیون خطی است که تلاش می کنیم آن را کاهش دهیم.
کاربرد رگرسیون خطی
رگرسیون خطی را می توان به عنوان روشی برای تجزیه و تحلیل آماری توصیف کرد که برای تحلیل نمرات توسط دانش آموزان بر اساس تعداد ساعت های مطالعه (در حالت ایده آل)- در اینجا نمرات کسب شده در امتحانات وابسته و تعداد ساعات مطالعه مستقل است.
پیش بینی عملکرد محصول بر اساس میزان بارندگی- عملکرد یک متغیر وابسته است در حالی که میزان بارش یک متغیر مستقل است.
پیش بینی حقوق فرد براساس سال ها تجربه- بنابراین، تجربه متغییر مستقل می شود در حالی که حقوق به متغیر وابسته تبدیل می شود. در ادامه به بررسی چند کاربرد هم رگرسیون خطی می پردازیم.
خط روند (Trend line)
محاسبه یک خط روند نشان دهنده یک پیشرفت یک فرآیند است، مانند حرکت بلند مدت در داده های سری زمانی پس از در نظر گرفتن سایر اجزا. این نشان می دهد که آیا مجموعه داده خاصی (مثلاً تولید ناخالص داخلی، قیمت نفت یا قیمت سهام) در طول زمان افزایش یا کاهش یافته است. خط روند را می توان به سادگی با چشم از طریق مجموعه ای از نقاط داده ترسیم کرد، اما موقعیت و شیب آن ها به درستی با استفاده از تکنیک های آماری مانند رگرسیون خطی محاسبه می شود. خطوط روند معمولاً خطوط مستقیم هستند، اگرچه برخی تغییرات بسته به میزان انحنای مورد نظر در خط، از چند جمله ای درجه بالاتری استفاده می کنند.
خطوط روند گاهی در تجزیه و تحلیل کسب و کار برای نشان دادن تغییرات داده ها در طول زمان استفاده می شود. رگرسیون خطی مزیت ساده بودن را دارد. خطوط روند اغلب برای بحث در مورد اینکه یک اقدام یا رویداد خاص (مانند آموزش یا کمپین تبلیغاتی) باعث تغییرات مشاهده شده در یک مقطع زمانی شده است، استفاده می شود. این یک تکنیک ساده است و نیازی به گروه کنترل، طراحی تجربی یا تکنیک تجزیه و تحلیل پیچیده ندارد.
Epidemiology
شواهد اولیه مربوط به مصرف دخانیات و ارتباط آن با مرگ و میر و بیماری از مطالعات مشاهده ای با استفاده از تحلیل رگرسیون بدست آمد. به منظور کاهش همبستگی های دروغین هنگام تجزیه و تحلیل داده های مشاهده ای، محققان معمولاً چندین متغیر را در مدل های رگرسیونی خود علاوه بر متغیر مورد علاقه اصلی قرار می دهند. به عنوان مثال، در یک مدل رگرسیونی که در آن سیگار کشیدن متغیر مستقل مورد علاقه اصلی است و متغیر وابسته طول عمر بر حسب سال اندازه گیری می شود، محققان ممکن است تحصیلات و درآمد را به عنوان متغیرهای مستقل اضافی در نظر بگیرند تا اطمینان حاصل شود که هرگونه تأثیر مشاهده شده بر طول عمر از سیگار است نه به دلیل عوامل اقتصادی و اجتماعی دیگر؛ با این حال، هرگز نمی توان همه متغیرهای پر از نویز احتمالی را در تجزیه و تحلیل تجربی گنجاند.
مالی
سرمایه گذاری، مدل قیمت گذاری دارایی های سرمایه ای از رگرسیون خطی و همچنین مفهوم بتا برای تجزیه و تحلیل و تعیین ریسک سیستماتیک یک سرمایه گذاری استفاده می کنند. این امر مستقیماً از ضریب بتا مدل رگرسیون خطی ناشی می شود که بازده سرمایه گذاری را به بازده تمام دارایی های خطرناک مرتبط می کند.
اقتصاد
اقتصادسنجی رگرسیون خطی ابزار تجربی غالب در اقتصاد است. برای مثال، برای پیش بینی هزینه های مصرف، هزینه های سرمایه گذاری ثابت، سرمایه گذاری موجودی مورد استفاده قرار می گیرد.
علم محیط زیست
رگرسیون خطی در طیف وسیعی از کاربردهای علوم محیطی کاربرد دارد.
یادگیری ماشین
رگرسیون خطی نقش مهمی در زیر حوزه هوش مصنوعی دارد که به یادگیری ماشین معروف است. الگوریتم رگرسیون خطی به دلیل سادگی نسبی و خواص شناخته شده، یکی از الگوریتم های اصلی یادگیری ماشین تحت نظارت است.
مزایای رگرسیون خطی
مزایای رگرسیون خطی ، پیاده سازی ساده رگرسیون خطی بسیار ساده است که می تواند به راحتی اجرا شود و نتایج رضایت بخشی را ارائه دهد. علاوه بر این، این نمونه مدل ها را می توان به راحتی و به صورت کارآمد حتی در سیستم هایی با قدرت محاسباتی نسبتاً پایین در مقایسه با سایر الگوریتم های پیچیده آموزش داد. رگرسیون خطی، پیچیدگی زمانی کمتری در مقایسه با برخی دیگر از الگوریتم های یادگیری ماشین دارد. معادلات ریاضی رگرسیون خطی نیز به راحتی قابل درک و تفسیر هستند. بنابراین تسلط بر رگرسیون خطی بسیار آسان است. عملکرد رگرسیون خطی در مجموعه های داده جداگانه خطی تقریباً متناسب با مجموعه داده های خطی است و اغلب برای یافتن ماهیت رابطه بین متغیرها استفاده می شود.
در رگرسیون خطی با سازمان دهی داده ها می توانیم کاهش Overfitting داشته باشیم. بیش برازش یا Overfitting زمانی اتفاق می افتد که مدل آموزشی ما بیش از حد داده ها آموزش را یاد گرفته و نمی تواند مقدار مناسبی برای داده های جدید پیش بینی کند.
معایب رگرسیون خطی
معایب رگرسیون خطی، رگرسیون خطی مستعد Underfitting است: در Underfitting وضعیتی ایجاد می شود که یک مدل یادگیری ماشین نتواند داده ها را به درستی ضبط کند. این معمولاً زمانی رخ می دهد که تابع نمی تواند داده ها را به خوبی سازمان دهی کند. از آنجا که رگرسیون خطی، رابطه خطی بین متغیرهای ورودی و خروجی را در نظر می گیرد، نمی تواند مجموعه داده های پیچیده را به درستی سازمان دهی کند. در اکثر سناریوهای واقعی و داده های موجود، رابطه بین متغیرهای مجموعه داده خطی نیست و بنابراین یک خط مستقیم با داده ها به درستی مطابقت ندارد. در چنین شرایطی یک تابع پیچیده تر می تواند داده ها را به طور موثرتری تحلیل کند. به همین دلیل مدل های رگرسیون خطی دارای دقت پایینی هستند.
این الگوریتم همچنین به داده های پرت شدیداً حساس است؛ این داده ها، داده هایی هستند که از سایر نقاط داده منحرف می شوند. داده های پرت می توانند به عملکرد مدل یادگیری ماشین به شدت آسیب برساند و اغلب می تواند منجر به مدل های کم دقت شوند.
نویز ها و داده های پرت می توانند تأثیر بسیار زیادی بر عملکرد رگرسیون خطی داشته باشند و بنابراین باید قبل از اعمال رگرسیون خطی بر روی مجموعه داده، به طور مناسب مدیریت شوند.
جمع بندی رگرسیون خطی
رگرسیون خطی یک الگوریتم است که همه علاقه مندان به یادگیری ماشین باید بدانند و همچنین الگوریتم مناسبی برای شروع افرادی است که می خواهند یادگیری ماشین را نیز بیاموزند. این الگوریتم در عین سادگی، توانایی بالایی در تحلیل داده های خطی دارد و نیازی به سیستم هایی با قدرت بالا ندارد.رگرسیون خطی به قطع یکی از مفید ترین الگوریتم های یادگیری ماشین است.
نویسنده: تیم پژوهش راهبرد
منابع
iq.opengenus.org
towardsdatascience.com

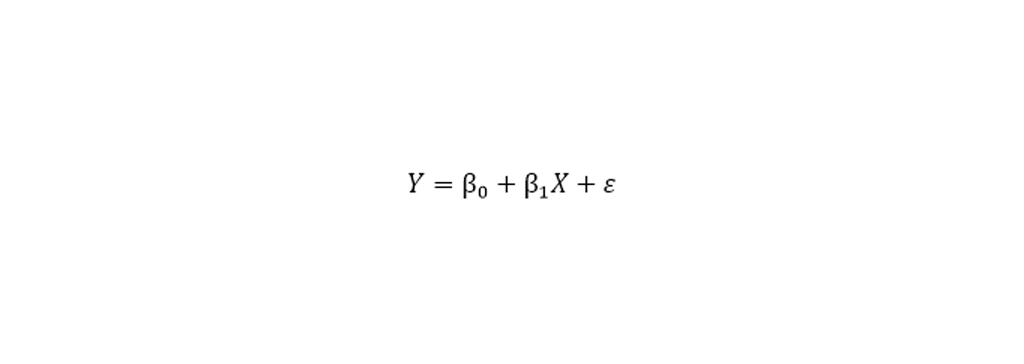
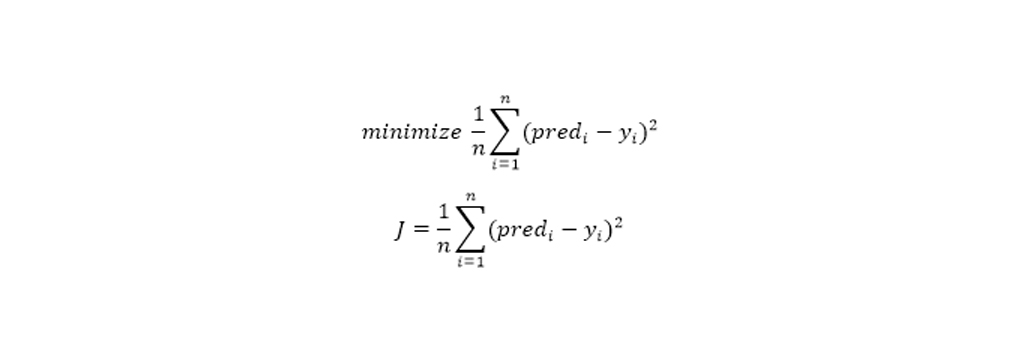
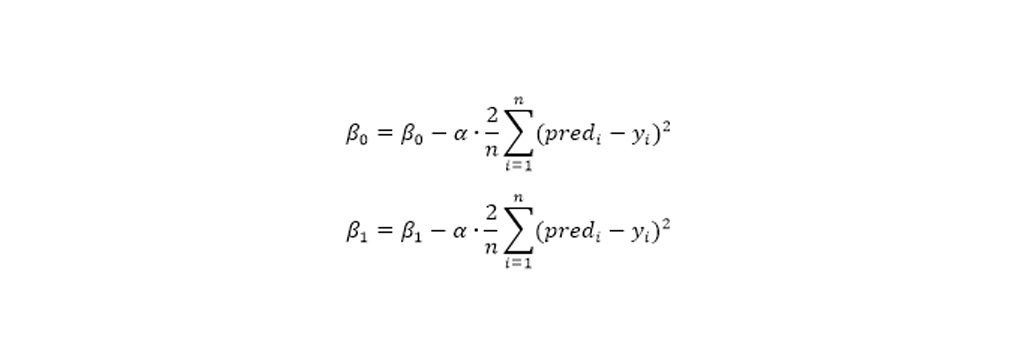




دیدگاهتان را بنویسید